Next: Nullfolgen Up: Folgen, rekursive Definition von Previous: Aufgaben:
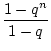 .
.
Hinzugefügten (zum unmittelbar vorhergehenden Zuwachs) derart vergrößert wird, dass das Hinzugefügte immer dieselbe Größe umfaßt, wird die (auszufüllende) Größe zu Ende gebracht, weil jedes Begrenzte durch jedes Abgegrenzte erschöpft wird (nämlich, wenn dieses oft genug von jenem weggenommen wird).
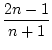
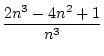
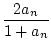 ist für alle
n
ist für alle
n