Definition 1.2.1
Eine Funktion
f : 
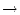
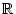 heißt reelle Zahlenfolge.
heißt reelle Zahlenfolge.
Bezeichnung: Ist
f (n) = an, so bezeichnen wir die
Folge auch mit (an).
Beispiele:
-
f :

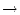
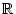 , f (n) =
, f (n) = 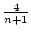 .
.
-
f (n) = (- 1)n . 2n.
- f (1) = 1 und
f (n + 1) = f (n) für alle
n

 .
.
- f (1) = 1 und
f (n + 1) = f (n) + (n + 1).
- f (1) = 1 und
f (n + 1) =
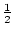 f (n).
f (n).
- f (1) = 2 und
f (n + 1) = f (n) + f (1).
Berechne jeweils eine Wertetabelle und zeichne den
Graph der Folge.
Definition 1.2.2
Eine Funktion
f : A 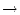 B heißt monoton wachsend,
wenn für alle
a, b
B heißt monoton wachsend,
wenn für alle
a, b  A gilt:
a
A gilt:
a b
b f (a)
f (a) f (b).
Eine Folge heißt monoton wachsend, wenn für alle
n
f (b).
Eine Folge heißt monoton wachsend, wenn für alle
n 
 gilt
an < an+1
gilt
an < an+1
Beispiele:
f : [0,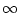 [
[ 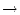
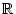 ,
f (x) = x2 ist monoton
wachsend.
Entsprechend erklärt man den Begriff ,,monoton fallend``
,
f (x) = x2 ist monoton
wachsend.
Entsprechend erklärt man den Begriff ,,monoton fallend``
Definition 1.2.3
Eine Funktion
f : A 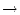 B heißt echt monoton wachsend,
wenn für alle a < b auch
f (a) < f (b) gilt.
Ungleichheitszeichen bleiben also erhalten.
B heißt echt monoton wachsend,
wenn für alle a < b auch
f (a) < f (b) gilt.
Ungleichheitszeichen bleiben also erhalten.
Definition 1.2.4
Eine Menge M von reellen Zahlen heißt nach oben beschränkt,
wenn es ein
os 
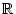 gibt, so dass für alle x
gibt, so dass für alle x  M gilt: x
M gilt: x os.
M heißt nach unten beschränkt, wenn es ein us gibt,
so dass für alle y
os.
M heißt nach unten beschränkt, wenn es ein us gibt,
so dass für alle y  Mgilt: us
Mgilt: us y.
y.
Ist die Welt der natürlichen Zahlen innerhalb des
Raumes der reellen Zahlen beschränkt, oder ist sie
durch eine undurchdringliche Mauer abgeschlossen
jenseits der es keine einzige natürliche Zahl, das
heißt Zählzahl gibt. Gibt es anders ausgedrückt in
der Welt der reellen Zahlen Individuen, die durch
noch so langes Zählen, seit dem Urknall nicht zu
erreichen sind. Archimedes von Syrakus (geb. um 287 vor Ch.
gest. 212 vor Ch.)
war
sogenannter Zähloptimist. Er behauptete Nein!. Bist
du nur fleißig genug, so erreichst du schließlich
jede Zahl, wenn nicht in diesem, dann in jenem
Leben. Unereichbare unendlich große Zahlen gibt es
nicht. Oder man könnte sagen, er war Zähldemokrat.
Vor der Unendlichkeit sind alle Zahlemn gleich. Die
Zahlen sind eine klassenlose Gesellschaft.
Von ihm stammt folgender Satz:
Beweis:1.
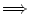 2.:
Sei h > 0 und c eine sehr große Zahl. Nach Teil 1.
kann
2.:
Sei h > 0 und c eine sehr große Zahl. Nach Teil 1.
kann
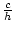 keine obere Schranke von
keine obere Schranke von
 sein. Also gibt
es ein
n
sein. Also gibt
es ein
n 
 mit
n >
mit
n > 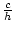 damit ist
n . h > c.
Das war zu zeigen.
damit ist
n . h > c.
Das war zu zeigen.
2.
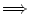 3.
Sei h eine winzig kleine Zahl. Dann gibt es ein
n
3.
Sei h eine winzig kleine Zahl. Dann gibt es ein
n 
 mit
n . h > 1. Damit ist
mit
n . h > 1. Damit ist
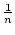 < h.
< h.
3.
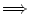 1.:
Sei c beliebig aus der Menge der positiven reellen
Zahlen. Wir zeigen: c kann keine obere Schranke von
1.:
Sei c beliebig aus der Menge der positiven reellen
Zahlen. Wir zeigen: c kann keine obere Schranke von
 sein. Es ist
sein. Es ist
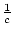 > 0. Also gibt es nach Teil 3.
ein
n
> 0. Also gibt es nach Teil 3.
ein
n 
 mit
mit
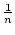 <
< 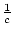 . Damit ist c < n. Und daher
ist c keine obere Schranke von
. Damit ist c < n. Und daher
ist c keine obere Schranke von
 .
.
1.
 4.:
Da die Äquivalenz von 1.,2. 3. schon gezeigt worden
ist, kann 2. und 3. mitverwendet werden. Wir zeigen
die Behauptung nur für positive Zahlen a < b. Der
Rest kann sich jeder einfach selber überlegen.
Sei also
0 < a < b. Nun gibt es nach Teil 3) eine
natürliche Zahl
n
4.:
Da die Äquivalenz von 1.,2. 3. schon gezeigt worden
ist, kann 2. und 3. mitverwendet werden. Wir zeigen
die Behauptung nur für positive Zahlen a < b. Der
Rest kann sich jeder einfach selber überlegen.
Sei also
0 < a < b. Nun gibt es nach Teil 3) eine
natürliche Zahl
n 
 , so dass
, so dass
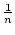 < b - a ist.
Auf dieses
< b - a ist.
Auf dieses
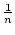 wenden wir die Eigenschaft 2) an. Es
gibt also ein kleinstes m, so dass
m .
wenden wir die Eigenschaft 2) an. Es
gibt also ein kleinstes m, so dass
m . 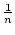
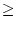 a ist.
Wäre
m .
a ist.
Wäre
m . 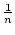 > b, so wäre
m .
> b, so wäre
m . 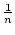 -
- 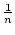 = (m - 1) .
= (m - 1) . 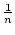 > b -
> b - 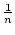 > b - (b - a) = a. Das ist aber ein Widerspruch.
Also gilt
a
> b - (b - a) = a. Das ist aber ein Widerspruch.
Also gilt
a
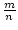 < b . Das wurde behauptet.
< b . Das wurde behauptet.
4.
 1.: Ist klar.
1.: Ist klar. 
Zitate:
,,Wenn ich die kurze Dauer meines Lebens betrachte,
verschlungen in die Ewigkeit, die ihm vorangeht und
ihm folgt, den kleinen Raum, den ich ausfülle, und
selbst jenen, den ich erblicke, der in der
grenzenlosen Weite der Räume versinkt, von denen
ich nichts weiß und die von mir nichts wissen, dann
erschrecke ich und wundere mich darüber, dass ich
nicht eher hier als dort erlebe; denn es gibt keinen
Grund, warum ich eher hier bin als dort; warum eher
jetzt als früher einmal`` Blaise Pascal:Le coeur et
ses raisons.
- Berechne die ersten 10 Glieder der Folge (an)
und zeichne den Graph der Folge:
(a) (an) =  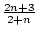 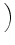 . . |
(b) (an) = 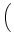 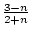 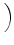 . . |
(c) (an) = (1 + 5 . (- 1)n . 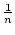 ) ) |
(d)(an) = 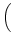  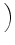 . . |
- Durch die Rekursionsvorschrift a1 : = 3,
an+1 : =
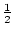 . (an +
. (an + 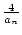 ) für alle
n
) für alle
n 
 ist eine Folge an definiert.
Berechnen Sie die ersten 8
Glieder der Folge und zeichnen Sie den Graphen der
Folge.
ist eine Folge an definiert.
Berechnen Sie die ersten 8
Glieder der Folge und zeichnen Sie den Graphen der
Folge.
- Die Folge (an), die durch die rekursive Definition
a1 : = 1, a2 : = 1 und
an+2 : = an+1 + an heißt Fibionacci
(Sohn des Bonacci) Folge.
Eigentlich hieß er Leonardo von Pisa geboren um 1170 gestorben um
1250. Er eignete sich auf einer Handelsreise in den Orient das grieschiche
und arabische mathematische Wiseen seiner Zeit an. Er war der erste, der
konsequent die arabischen Ziffern verwendetet. Damit zeigte er die Vorteile
des dekadischen Stellenwertsystems. Er leß als erster den Grauch der
,,0`` zu. Er löste al erster kubische Gleichungen und führte damit weit seiner
Zeit voraus die Mathematik auf fruchtbaren Boden.
Bestimme die ersten 15 Glieder der Folge. Beweise
die folgenden Beziehungen zwischen den Gliedern der
Folge.
-
a1 + a3 +...+ a2n+1 = a2n+2
-
a12 + a22 +...+ an2 = an . an+1.
-
1 + a1 + a2 +...+ an = an+2.
- Wieviel Lösungen hat die Gleichung?
-
X + Y + Z = 1992 mit
X, Y, Z

 ?
?
-
X + 5Y = 1992 mit
X, Y

 ?
?
-
3X + 2Y = 1992 mit
X, Y

 .
.
- Untersuche ob die Folgen monoton wachsend beziehungsweise
monoton fallend oder keins von beidem
sind.
(a)
(an) = 
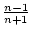
 . (b)
(an) = (n2 + 2n - 1).
. (b)
(an) = (n2 + 2n - 1).
(c)
(an) = 
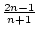
 . (d)
(an) =
. (d)
(an) = 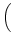
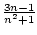
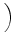 .
.
(e)
(an) = (n3 -2n2).
Definition 1.2.5
Eine Folge (an) heißt arithmetisch,
wenn
die Differenz aufeinanderfolgender Folgenglieder
stets konstant ist. Wenn es also ein
d 
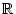 gibt
mit
d = an+1 - an für alle
n
gibt
mit
d = an+1 - an für alle
n 
 .
.
Unterabschnitte
Andreas Bartholome
2003-11-26
![]() [
[ ![]()
![]() ,
f (x) = x2 ist monoton
wachsend.
Entsprechend erklärt man den Begriff ,,monoton fallend``
,
f (x) = x2 ist monoton
wachsend.
Entsprechend erklärt man den Begriff ,,monoton fallend``
![]() 3.
Sei h eine winzig kleine Zahl. Dann gibt es ein
n
3.
Sei h eine winzig kleine Zahl. Dann gibt es ein
n ![]()
![]() mit
n . h > 1. Damit ist
mit
n . h > 1. Damit ist
![]() < h.
< h.
![]() 1.:
Sei c beliebig aus der Menge der positiven reellen
Zahlen. Wir zeigen: c kann keine obere Schranke von
1.:
Sei c beliebig aus der Menge der positiven reellen
Zahlen. Wir zeigen: c kann keine obere Schranke von
![]() sein. Es ist
sein. Es ist
![]() > 0. Also gibt es nach Teil 3.
ein
n
> 0. Also gibt es nach Teil 3.
ein
n ![]()
![]() mit
mit
![]() <
< ![]() . Damit ist c < n. Und daher
ist c keine obere Schranke von
. Damit ist c < n. Und daher
ist c keine obere Schranke von
![]() .
.
![]() 4.:
Da die Äquivalenz von 1.,2. 3. schon gezeigt worden
ist, kann 2. und 3. mitverwendet werden. Wir zeigen
die Behauptung nur für positive Zahlen a < b. Der
Rest kann sich jeder einfach selber überlegen.
Sei also
0 < a < b. Nun gibt es nach Teil 3) eine
natürliche Zahl
n
4.:
Da die Äquivalenz von 1.,2. 3. schon gezeigt worden
ist, kann 2. und 3. mitverwendet werden. Wir zeigen
die Behauptung nur für positive Zahlen a < b. Der
Rest kann sich jeder einfach selber überlegen.
Sei also
0 < a < b. Nun gibt es nach Teil 3) eine
natürliche Zahl
n ![]()
![]() , so dass
, so dass
![]() < b - a ist.
Auf dieses
< b - a ist.
Auf dieses
![]() wenden wir die Eigenschaft 2) an. Es
gibt also ein kleinstes m, so dass
m .
wenden wir die Eigenschaft 2) an. Es
gibt also ein kleinstes m, so dass
m . ![]()
![]() a ist.
Wäre
m .
a ist.
Wäre
m . ![]() > b, so wäre
m .
> b, so wäre
m . ![]() -
- ![]() = (m - 1) .
= (m - 1) . ![]() > b -
> b - ![]() > b - (b - a) = a. Das ist aber ein Widerspruch.
Also gilt
a
> b - (b - a) = a. Das ist aber ein Widerspruch.
Also gilt
a![]()
![]() < b . Das wurde behauptet.
< b . Das wurde behauptet.
![]() 1.: Ist klar.
1.: Ist klar. ![]()
![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]() )
)![]()
![]()
![]() .
.![]()
![]()
![]() . (b)
(an) = (n2 + 2n - 1).
. (b)
(an) = (n2 + 2n - 1).
![]()
![]()
![]() . (d)
(an) =
. (d)
(an) = ![]()
![]()
![]() .
.