Next: Globale Stetigkeit Up: Definition und Beispiele Previous: Beispiele:
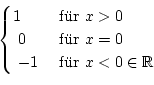
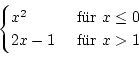 .
.
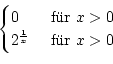

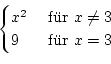
f : ![]()
![]() x
x ![]() [x] +
[x] + ![]() .
.
|
|
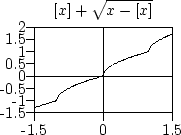
Man zeige
f (x) = [x] + monoton steigend und stetig für alle
x
f (x) = [x] -
auf Stetigkeit. |
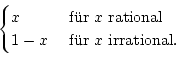 Diese Funktion ist nur für a = 0.5 stetig.
Es gibt aber zu jedem
y
Diese Funktion ist nur für a = 0.5 stetig.
Es gibt aber zu jedem
y