Next: Aufgaben: Up: Definition und Beispiele Previous: Definition und Beispiele
![\includegraphics[height=5cm width=5cm]{/home/andreas/tex/schule/elfte/bild/bild2}](img187.png)
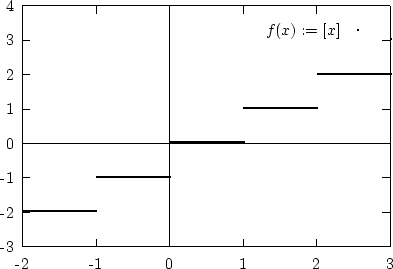
f (x) = 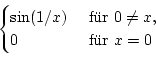 |
Ihr Graph sieht so aus:
![\includegraphics[height=5cm width=10cm]{/home/andreas/tex/schule/elfte/bild/bild3}](img191.png)
Das ist um den Nullpunkt herum ziemlich wild. Schauen wir es mit der Lupe an:
![\includegraphics[height=5cm width=10cm]{/home/andreas/tex/schule/elfte/bild/bild4}](img192.png)
Beweis:Sei
(an) = (![]() ). Dann ist
). Dann ist
![]() (an) = 0.
Es ist
(an) = 0.
Es ist
![]() f (an) = lim 1 = 1.
Aber es ist f (0) = 0. Daher ist die Funktion unstetig bei 0.
f (an) = lim 1 = 1.
Aber es ist f (0) = 0. Daher ist die Funktion unstetig bei 0. ![]()
Lag es vielleicht nur daran wie wir f (0) definiert haben? Untersuche das!
Es gibt also durchaus unstetige Funktionen. Wer aber vor diesem Beispiel vermutet hat, dass es nur stetige Funktionen gibt, braucht sich nicht zu schämen. Einer der berühmtesten Mathematiker, später das Urbild an Genauigkeit, Karl Weierstraß (geb. 31.10. 1815 und gst. 19.2. 1897) war in einer seiner ersten akademischen Vorlesung noch dieser Ansicht. So stammt aus einer Mitschrift einer Vorlesung, die wahrscheinlich 1859 gehalten wurde folgender Satz: ,,Jede Function ist stetig veränderlich, wenn ihr Argument veränderlich ist; und es ist dies folgendermaßen zu definieren: Wenn man dem Argumente einer Function einen Werth zufügt, der so klein ist, als man ihn nur denken kann, so erleidet die Function eine Änderung, welche ebenfalls so klein ist, dass man sie sich kaum vorstellen kann`` (zitiert nach R. Bölling ,,Karl Weierstraß- Stationen eines Lebens`` [#!Boelling!#, Seite 65]) Wir sehen diese Definition ist noch voller nebulöser, undeutlicher Worte. Wie klein kannst du dir eine Zahl denken? Kann man sie sich noch kleiner vorstellen?
Weierstraß selber war es, der schließlich den entscheidenden Schritt zum Verständnis von Grenzwert und Stetigkeit machte. Von ihm stammt die Auffassung der Analysis, wie wir sie heute haben. Aber ganz so Unrecht hatte andererseits Weierstraß mit seiner obigen Aussage nicht. Damals war nämlich der Begriff der Funktion nicht vollständig geklärt. Man dachte nur an ,,vernünftige Funktionen``, die man durch einen algebraischen Ausdruck (Limes Zeichen durften auch vorkommen) hinschreiben kann. In diesem Sinne belegt der nächste Satz, dass Weierstraß doch so ungefähr Recht hatte.
![]() : A
: A ![]() x
x ![]()
![]()
![]()
![]() stetig an der Stelle a.
stetig an der Stelle a.
Die Funktion
f : ![]()
![]() x
x ![]()
 ist an der Stelle 0 unstetig.
Aber sie ist noch beschränkt.
Bei einer Nullfolge haben wir gesehen, dass das Produkt aus einer
beschränkten Folge und einer Nullfolge beschränkt ist.
So kann man auch hier die Funktion durch einen
geeigneten Faktor stetig an der Stelle 0 machen.
Wir betrachten
ist an der Stelle 0 unstetig.
Aber sie ist noch beschränkt.
Bei einer Nullfolge haben wir gesehen, dass das Produkt aus einer
beschränkten Folge und einer Nullfolge beschränkt ist.
So kann man auch hier die Funktion durch einen
geeigneten Faktor stetig an der Stelle 0 machen.
Wir betrachten
g :  |
Diese Funktion ist an der Stelle 0 stetig. Man sieht es dem Graphen an.
![\includegraphics[height=5cm width=10cm]{/home/andreas/tex/schule/elfte/bild/bild5}](img203.png)
![\includegraphics[height=5cm width=10cm]{/home/andreas/tex/schule/elfte/bild/bild6}](img204.png)
Man kann die auch exakt begründen. Sei dazu (an) eine Nullfolge.
Dann ist
sin(1/an) eine beschränkte Folge.
Also ist
![]() an . sin(1/an) = 0 = g(0).
Dies war zu zeigen.
Mit Hilfe des Satzes 2.1.1, erkennt man, dass unter anderem
jedes Polynom
für jeden Punkt in
an . sin(1/an) = 0 = g(0).
Dies war zu zeigen.
Mit Hilfe des Satzes 2.1.1, erkennt man, dass unter anderem
jedes Polynom
für jeden Punkt in
![]() stetig ist.
stetig ist.