Globale Stetigkeit
Definition 2.2.1
Ein Funktion
f : [a, b] 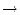
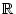 heißt stetig auf dem Intervall, wenn
sie für alle
c
heißt stetig auf dem Intervall, wenn
sie für alle
c 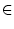 [a, b] stetig ist..
[a, b] stetig ist..
Anschaulisch besagt dieser Satz: Zeichnet man den Graphen einer stetigen
Funktion, beginnt dabei im Negativen und endet im Positiven, so hat man einmal
die Nullinie überquert.
Graphen stetiger Funktionen können ohne abzusetzen gezeichnet werden.
Beweis:Wir liefern einen ganz konstruktiven Beweis.
Wir setzen voraus, dass f (a) < 0 und f (b) > 0 ist.
Nun definieren wir induktiv drei Folgen.
a0 : = a, b0 : = b und
m0 : = (a0 + b0)/2.
Wir nehmen an mn sei schon definiert. Es sei:
an+1 : = 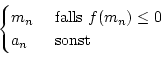
bn+1 : = 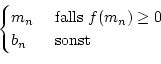
an ist monoton wachsend und nach oben beschränkt und daher konvergent.
Genauso ist bn monoton fallend und nach unten beschränkt und daher
konvergent.
Weiterhin ist
bn - an = 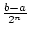 . Also ist bn - an eine
Nullfolge. Sei
c =
. Also ist bn - an eine
Nullfolge. Sei
c = 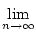 an =
an = 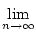 bn.
Da f stetig ist, ist
f (c) =
bn.
Da f stetig ist, ist
f (c) = 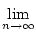 f (an)
f (an)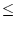 0.
Andererseits ist
f (c) =
0.
Andererseits ist
f (c) = 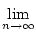 f (bn)
f (bn)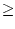 0.
Daher ist f (c) = 0.
0.
Daher ist f (c) = 0. 
Diesen Beweis kann man fast wörtlich in ein Programm zur Berechnung von
Nullstellen übersetzen.
Der Beweis ist uns an dieser Stelle zu schwer.
Andreas Bartholome
2003-11-26
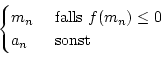
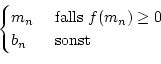
![]() . Also ist bn - an eine
Nullfolge. Sei
c =
. Also ist bn - an eine
Nullfolge. Sei
c = ![]() an =
an = ![]() bn.
Da f stetig ist, ist
f (c) =
bn.
Da f stetig ist, ist
f (c) = ![]() f (an)
f (an)![]() 0.
Andererseits ist
f (c) =
0.
Andererseits ist
f (c) = ![]() f (bn)
f (bn)![]() 0.
Daher ist f (c) = 0.
0.
Daher ist f (c) = 0. ![]()