Die Folge
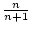 strebt gegen 1 wie jeder leicht
,,sieht``.
strebt gegen 1 wie jeder leicht
,,sieht``.
Definition 1.2.9
Eine Folge (an) hat den Grenzwert a genau dann, wenn
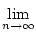 | a - an| = 0 ist.
Man schreibt:
| a - an| = 0 ist.
Man schreibt:
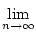 (an) = a.
(an) = a.
Satz 1.2.5
Jede konvergente Folge hat nur einen Grenzwert.
Beweis:Angenommen die konvergente Folge (an) hätte zwei
Grenzwerte a < b.
Dann sind nach Definition die Folgen (a - an) und (b - an) Nullfolgen.
Also ist
((b - an) - (a - an)) = (b - a) eine Nullfolge.
Dies kann aber nicht sein. 
Beweis:
((a + b) - (an + bn)) = (a - an) + (b - bn). Beide Summanden
sind Nullfolgen. Daraus ergibt sich mit der
Definition die Behauptung. 
Satz 1.2.7
Jede konvergente Folge ist beschränkt.
Beweis:Sei (an) eine konvergente Folge mit
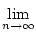 (an) = a.
Dann ist
| an - a + a|
(an) = a.
Dann ist
| an - a + a| | a - an| + | a|.
Der erste Summand ist beschränkt, da er eine Nullfolge ist.
Der zweite ist sowieso beschränkt. Daraus ergibt
sich die Behauptung.
| a - an| + | a|.
Der erste Summand ist beschränkt, da er eine Nullfolge ist.
Der zweite ist sowieso beschränkt. Daraus ergibt
sich die Behauptung. 
Satz 1.2.8
Sind (an) und (bn) konvergente Folgen, dann ist die
Folge
(an . bn) konvergent und es gilt:
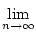 (anbn) =
(anbn) = 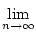 (an)
(an)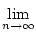 (bn).
(bn).
Beweis:
| a . b - anbn| = | ab - anb + anb - anbn| | a - an|| b| + | an|| b - bn|. Nun sind beide Summanden
Produkte aus einer beschränkten
Folge und einer Nullfolge. Damit ist
| a . b - anbn| eine Nullfolge.
| a - an|| b| + | an|| b - bn|. Nun sind beide Summanden
Produkte aus einer beschränkten
Folge und einer Nullfolge. Damit ist
| a . b - anbn| eine Nullfolge. 
Satz 1.2.9
Sei (an) eine konvergente Folge und
a = 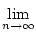 (an)
(an) 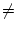 0.
Dann ist
0.
Dann ist
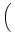
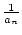
 konvergent und es
ist
konvergent und es
ist
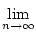
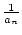 =
= 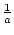 .
.
Beweis:Wir setzen zunächst a > 0 voraus. Ich zeige
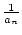 ist
beschränkt. Ist s irgend eine Zahl 0 < s < a. Für
fast alle Folgenglieder gilt:
ist
beschränkt. Ist s irgend eine Zahl 0 < s < a. Für
fast alle Folgenglieder gilt:
0 < s < an < a + (a - s). Damit gilt für fast alle
n 
 :
:
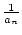 <
< 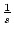 .
Die endlich vielen Folgenglieder, die
diese Ungleichung nicht erfüllen sind erst recht
beschränkt, denn jede endliche Menge ist
beschränkt. Also ist die Folge
.
Die endlich vielen Folgenglieder, die
diese Ungleichung nicht erfüllen sind erst recht
beschränkt, denn jede endliche Menge ist
beschränkt. Also ist die Folge
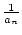 beschränkt. Nun ist :
beschränkt. Nun ist :
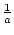 -
- 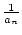
 =
= 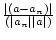 . Das Produkt
aus etwas beschränktem und einer Nullfolge ist eine
Nullfolge.
. Das Produkt
aus etwas beschränktem und einer Nullfolge ist eine
Nullfolge. 
Unterabschnitte
Andreas Bartholome
2003-11-26
![]() (an + bn) = a + b.
(an + bn) = a + b.![]()
![]() :
:
![]() <
< ![]() .
Die endlich vielen Folgenglieder, die
diese Ungleichung nicht erfüllen sind erst recht
beschränkt, denn jede endliche Menge ist
beschränkt. Also ist die Folge
.
Die endlich vielen Folgenglieder, die
diese Ungleichung nicht erfüllen sind erst recht
beschränkt, denn jede endliche Menge ist
beschränkt. Also ist die Folge
![]() beschränkt. Nun ist :
beschränkt. Nun ist :
![]()
![]() -
- ![]()
![]() =
= ![]() . Das Produkt
aus etwas beschränktem und einer Nullfolge ist eine
Nullfolge.
. Das Produkt
aus etwas beschränktem und einer Nullfolge ist eine
Nullfolge. ![]()