Betrachten wir die Folge
(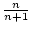 ) = (
) = (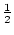 ,
,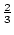 ,
,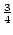 ,
,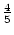 ,...).
Von ihr wissen wir, dass sie den Grenzwert 1 hat.
Suchen wir nur jedes zweite Glied der Folge aus, so erhalten wir
die Folge
(
,...).
Von ihr wissen wir, dass sie den Grenzwert 1 hat.
Suchen wir nur jedes zweite Glied der Folge aus, so erhalten wir
die Folge
(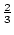 ,
,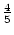 ,
,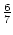 ,...) = (
,...) = (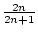 ).
Auch diese Folge hat den Grenzwert 1. Genausogut können wir jedes
10te Glied der Folge auswählen.
Dies ergibt
(
).
Auch diese Folge hat den Grenzwert 1. Genausogut können wir jedes
10te Glied der Folge auswählen.
Dies ergibt
(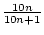 ).
).
Satz 1.2.10
Sei
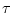 :
: 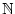
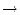
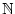 eine streng monoton wachsende
Funktion. Dann ist für alle
n
eine streng monoton wachsende
Funktion. Dann ist für alle
n 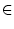
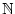 :
n
:
n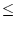
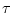 (n).
(n).
Beweis:Es ist sicher
1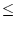
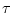 (1). Sei die Behauptung richtig
für k. Also es gelte
k
(1). Sei die Behauptung richtig
für k. Also es gelte
k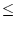
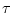 (k).
Da
(k).
Da 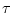 streng monoton wachsend ist, ist
k
streng monoton wachsend ist, ist
k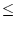
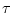 (k) <
(k) < 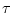 (k + 1).
Daher folgt:
k + 1
(k + 1).
Daher folgt:
k + 1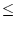
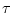 (k + 1).
(k + 1). 
Definition 1.2.10
Sei
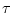 :
: 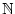
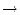
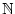 eine streng monotone Funktion und
(an) eine reelle Zahlenfolge. Die Folge
(a
eine streng monotone Funktion und
(an) eine reelle Zahlenfolge. Die Folge
(a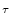 (n)) heißt dann Teilfolge von (an)
(n)) heißt dann Teilfolge von (an)
Satz 1.2.11
Jede Teilfolge einer konvergenten Folge ist konvergent
und hat den gleichen Grenzwert.
Beweis:Sei
a = 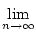 an. Weiter sei
an. Weiter sei
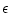 > 0 gegeben.
Dann gibt es ein
k
> 0 gegeben.
Dann gibt es ein
k 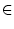
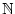 , so dass für alle n
, so dass für alle n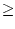 k gilt:
| a - an| <
k gilt:
| a - an| < 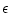 .
Nun ist für alle
n
.
Nun ist für alle
n 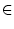
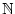 :
: 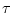 (n)
(n)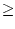 n.
Das heißt es gilt erst recht:
| a - a
n.
Das heißt es gilt erst recht:
| a - a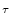 (n)| <
(n)| < 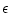 . Dies bedeutet, dass die Folge
(a
. Dies bedeutet, dass die Folge
(a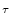 (n)) gegen a konvergiert.
(n)) gegen a konvergiert. 
Dieser Satz ist oft hilfreich, um den Grenzwert
einer Folge tatsächlich auszurechnen, wenn man weiß, dass die Folge
konvergiert.
Unterabschnitte
Andreas Bartholome
2003-11-26