Beispiele:
- Einstellige Algebren sind gut malbar. Ein paar habe ich gezeichnet. Es
sind gerichtete Graphen, bei denen von jedem Knoten genau ein Pfeil ausgeht (Siehe Abbildung 4).
Abbildung 4:
gerichtete Graphen
|
![\includegraphics[width=0.8\textwidth]{bilder/bilder-2}](img19.png) |
- Der Urzeithirte wird vielleicht seine Schafe folgendermaßen gezählt
haben. Für jedes Schaf legt er ein Hölzchen in den Sand. Er macht sich also
eine Strichliste ||||||....
Seine Funktion
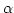 ist also ganz einfach: Einen Strich dranhängen.
Unser Ziffernsystem stammt von den Indern erfunden. Der Inder
Arybhatiya hat zum ersten Mal Regeln zum Rechnen im
Positionssystem angegeben. Darauf beruht die folgende raffinierte Methode
des Zählens.
ist also ganz einfach: Einen Strich dranhängen.
Unser Ziffernsystem stammt von den Indern erfunden. Der Inder
Arybhatiya hat zum ersten Mal Regeln zum Rechnen im
Positionssystem angegeben. Darauf beruht die folgende raffinierte Methode
des Zählens.
0, 1, 10,11, 100,...
Ein geistiger Nachfahre des berühmten Inders Aryabhata
hat sie erfunden. Siehe das Buch ,,Lexikon bedeutender Mathematiker``
[Got90, Seite 29]
- Berühmt sind die quadratischen Iterationen, die unter anderem die
sogenannten Feigenbaumdiagramme
ergeben.
Betrachten wir die logistische Funktion
 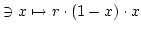 |
(1) |
Setzt man etwa 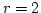 , so erhält man die linke Bahn von Abbildung 3
, so erhält man die linke Bahn von Abbildung 3
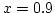 .
Setzt man etwa
.
Setzt man etwa 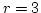 , so erhält man die rechte Bahn von Abbildung 3
, so erhält man die rechte Bahn von Abbildung 3
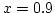 .
.
Abbildung 5:
Bahn eines Punktes unter der logistischen Funktion
|
![\includegraphics[height=0.3\textheight width=0.45\textwidth]{programme/bahn}](img26.png)
![\includegraphics[height=0.3\textheight width=0.45\textwidth]{programme/bahn2}](img27.png) |
Erklärung 2.2
Eine Teilmenge
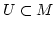 ist gegenüber der Abbildung
ist gegenüber der Abbildung
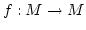 abgeschlossen, wenn
abgeschlossen, wenn
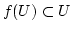 gilt. Sie ist
gilt. Sie ist 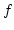 -koabgeschlossen, wenn
-koabgeschlossen, wenn
 ist.
ist.
![$ [U]$](img32.png) ist die Menge der Punkte, die von
ist die Menge der Punkte, die von 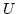 aus erreichbar sind durch
aus erreichbar sind durch 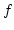 .
Besteht
.
Besteht 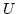 nur aus einem Element, so heißt
nur aus einem Element, so heißt ![$ [u]$](img34.png) die von
die von 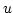 erzeugte Bahn.
Die leere Menge und die Menge
erzeugte Bahn.
Die leere Menge und die Menge 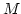 ist gegenüber jeder Abbildung der Menge in
sich abgeschlossen.
ist gegenüber jeder Abbildung der Menge in
sich abgeschlossen.
Beweis:Zu 1. Sei
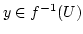 . Dann ist
. Dann ist 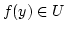 . Da
. Da 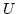 gegenüber
gegenüber 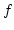 abgeschlossen ist, ist
abgeschlossen ist, ist
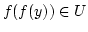 . Daher ist
. Daher ist
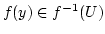 .
.
Zu 2. Sei
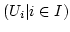 eine Familie von abgeschlossenen Mengen und
eine Familie von abgeschlossenen Mengen und
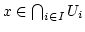 . Dann ist
. Dann ist
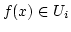 für alle
für alle 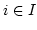 . Das
heißt
. Das
heißt
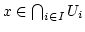
Zu 3. Der Durchschnitt aller abgeschlossenen Teilmengen, die 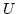 enthalten,
ist die kleinste abgschlossene Teilmenge, die
enthalten,
ist die kleinste abgschlossene Teilmenge, die 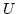 enthält.
enthält.
Zu 4. Sei
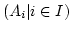 eine Familie von gegenüber
eine Familie von gegenüber 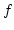 abgeschlossenen
Teilmengen. Weiter sei
abgeschlossenen
Teilmengen. Weiter sei 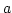 in
in
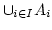 . Dann gibt es ein
. Dann gibt es ein 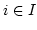 mit
mit
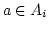 . Also ist
. Also ist
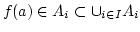 .
. 
Erklärung 2.3
Sei
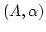 eine einstellige Algebra und
eine einstellige Algebra und
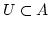 eine Teilmenge von
eine Teilmenge von  mit
mit
![$ [U]=A$](img53.png) . Dann heißt
. Dann heißt  Erzeugendensystem von
Erzeugendensystem von  . Man sagt
. Man sagt  erzeugt
erzeugt
 .
.
Beweis:Zu 1.:
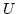 enthält
enthält
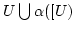 . Außerdem ist
. Außerdem ist
![$ U\bigcup \alpha([U])$](img60.png) abgeschlossen gegenüber
abgeschlossen gegenüber 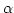 und enthält
und enthält 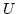 . Daher ist
. Daher ist
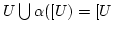 .
.
Zu 2.:
![$ \alpha([U])$](img62.png) ist abgeschlossen gegenüber
ist abgeschlossen gegenüber 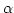 und enthält
und enthält 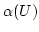 .
Also ist
.
Also ist
![$ \alpha([U]) =[\alpha(U)]$](img55.png) .
.
Zu 3.
In Worten kann man dies so fassen: Sind 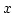 und
und 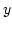 von
von 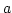 aus erreichbar, so
gibt es Punkte, die von
aus erreichbar, so
gibt es Punkte, die von 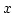 und
und 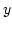 aus erreichbar sind.
aus erreichbar sind.
Es ist
![$ [x]\bigcap [a]=[x]\neq \emptyset$](img65.png) . Sei
. Sei
Es ist 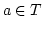 . Sei
. Sei 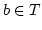 . Dann ist
. Dann ist
![$ [x]\bigcap [b]\neq \emptyset$](img69.png) .Es gibt also ein
.Es gibt also ein ![$ c \in [b]$](img70.png) mit
mit ![$ c\in [x]$](img71.png) .
Also ist
.
Also ist
![$ \alpha(c)\in [\alpha(b)]$](img72.png) und
und
![$ \alpha(c)\in [x]$](img73.png) .
. 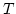 ist daher
gegenüber
ist daher
gegenüber 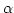 abgeschlossen. Also ist
abgeschlossen. Also ist ![$ T=[a]$](img75.png) .
. 
Andreas Bartholome
2005-03-06
![]() , so erhält man die linke Bahn von Abbildung 3
, so erhält man die linke Bahn von Abbildung 3
![]() .
Setzt man etwa
.
Setzt man etwa ![]() , so erhält man die rechte Bahn von Abbildung 3
, so erhält man die rechte Bahn von Abbildung 3
![]() .
.
![]() eine Familie von abgeschlossenen Mengen und
eine Familie von abgeschlossenen Mengen und
![]() . Dann ist
. Dann ist
![]() für alle
für alle ![]() . Das
heißt
. Das
heißt
![]()
![]() enthalten,
ist die kleinste abgschlossene Teilmenge, die
enthalten,
ist die kleinste abgschlossene Teilmenge, die ![]() enthält.
enthält.
![]() eine Familie von gegenüber
eine Familie von gegenüber ![]() abgeschlossenen
Teilmengen. Weiter sei
abgeschlossenen
Teilmengen. Weiter sei ![]() in
in
![]() . Dann gibt es ein
. Dann gibt es ein ![]() mit
mit
![]() . Also ist
. Also ist
![]() .
. ![]()
![]() ist abgeschlossen gegenüber
ist abgeschlossen gegenüber ![]() und enthält
und enthält ![]() .
Also ist
.
Also ist
![]() .
.
![]() und
und ![]() von
von ![]() aus erreichbar, so
gibt es Punkte, die von
aus erreichbar, so
gibt es Punkte, die von ![]() und
und ![]() aus erreichbar sind.
aus erreichbar sind.
![]() . Sei
. Sei