Sei g eine Gerade. Jedem Punkt P der Ebenen wird auf folgende Weise genau
ein Punkt P' zugeordnet.
- Liegt P auf g so ist P' = P.
- Liegt P nicht auf g, so liegt P auf dem Lot von P auf g.
Sei S der Schnittpunkt des Lotes von P auf g mit g.
Dann hat P' von S den gleichen Abstand wie P liegt aber auf der
anderen Seite.
P' heißt der Bildpunkt von P bei der Spiegelung an g. Wir bezeichnen ihn
auch mit Sg(P) = P'. (Spiegelpunkt von P bei Spiegelung an g).
Die Gerade g heißt auch Spiegelachse oder Symmetrieachse.
Satz 4.1.1
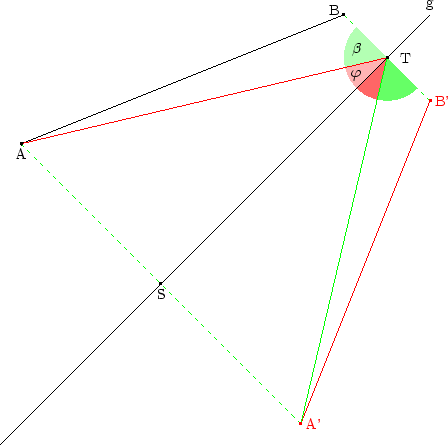
Sei g eine Gerade und A, B zwei Punkte. Ist Sg die Spiegelung an g,
so gilt
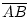 =
= 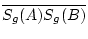 . Das heißt die
Gegenstandsstrecke ist genau so lang wie die Bildstrecke.
. Das heißt die
Gegenstandsstrecke ist genau so lang wie die Bildstrecke.
Beweis:Nach Konstruktion ist
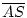 =
= 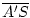 und
und
 AST =
AST =  A'ST = 900. Also ist wegen (SWS)
A'ST = 900. Also ist wegen (SWS)
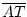 =
= 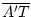 :
Daher ist
:
Daher ist
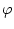 =
= 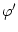 . Außerdem ist nach Konstruktion
. Außerdem ist nach Konstruktion
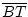 =
= 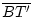 . Mit dem Satz (SWS) folgt, dass
. Mit dem Satz (SWS) folgt, dass
 ATB
ATB 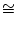
 A'TB' ist. Daher ist
A'TB' ist. Daher ist
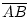 =
= 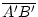 .
. 
Folgerung 4.1.2
Gegeben sei eine Achse g
- Bei der Achsenspiegelung ist das Bild einer Strecke [AB] die Strecke
[Sg(A)Sg(B)].
- Das Bild einer Geraden h ist eine Gerade.
- Gegenstands- und Bildwinkel sind gleich groß.
Beweis:Zu a: Liege C auf [AB]. Das heißt
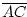 +
+ 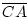 =
= 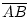 . Wegen Satz 4.1.1
folgt:
. Wegen Satz 4.1.1
folgt:
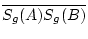 =
= 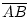 =
= 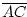 +
+ 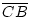 =
= 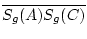 +
+ 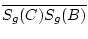 . Daher ist
. Daher ist
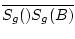 =
= 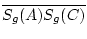 +
+ 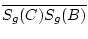 .
Daher ist
Sg(C)
.
Daher ist
Sg(C) 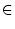 [Sg(A)Sg(B)]. Ist X ein Punkt von der Strecke
[Sg(A)Sg(B)], so ist
Sg(X)
[Sg(A)Sg(B)]. Ist X ein Punkt von der Strecke
[Sg(A)Sg(B)], so ist
Sg(X) 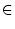 [AB] und dher
X = Sg(Sg(X))
[AB] und dher
X = Sg(Sg(X)) 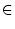 [Sg(A)Sg(B)]. Jeder Punkt der Strecke
Sg(A)Sg(B)] kommt daher
tatsächlich als Bildpunkt vor.
[Sg(A)Sg(B)]. Jeder Punkt der Strecke
Sg(A)Sg(B)] kommt daher
tatsächlich als Bildpunkt vor.
Zu b: Genauso.
Zu c: Überlege dies dir selbständig. 
Aufgaben:
- Spiegle ein beliebiges Dreieck an einer Geraden g.
- g schneidet das Dreieck nicht.
- g ist eine Dreiecksseite.
- g schneidet das Dreieck.
- Max schlägt folgende ,,Halbspiegelung`` vor. Gegeben ist die Gerade
g. Jedem Punkt P der Ebene wird genau ein Bildpunkt der Ebene
P' = Sg(P) zugeordnet. Liegt P auf g, so sei Sg(P) : = P. Liegt P
nicht auf g,
so fällt man das Lot von P auf die Gerade g. Es habe den Fußpunkt F.
Sg(P) liegt auf der Seite von g, welche P nicht enthält,
so dass
[Sg(P)F] genauso lang ist wie [PF].
- Zeichne das Bild eines beliebigen Dreiecks bei dieser
Halbspiegelung.
- Ist bei der Halbspiegelung die Bildstrecke genau so lang wie die
Gegenstandsstrecke?
- Ist der Bildwinkel bei diese Halbspiegelung genausogroß wei der Gegenstandswinkel?
- Konstruiere das Bild einer Gerade. Wieviel Bildpunkte muss man
konstruieren? Begründung!
- Konstruiere das Bild eines Kreises bei verschiedener Lage der Achse
zum Kreis.
- Zeige: Bei jeder Achsenspiegelung ist das Bild eines Kreise wieder
ein Kreis.
- Zeige:
- Ein gleichschenkliges Dreieck ist achsensymmetrisch. Was ist die
Symmetrieachse?
- Ein gleichseitiges DReieck hat drei Symmetrieachsen.
- Zwie sich schneidende Geraden bilden eine achsesymmetrische
Figur. Was sind die Symmetrieachsen?
- Zwei parallele Geraden bilden eine achsensymmetrische Figur. Was sind
die Symmetrieachsen?
- Konstruiere die Symmetriechsen zweier Geraden, deren Schnittpunkt
nicht auf dem Zeichenblatt liegt.
- Gegeben sind zwei symmetrische Punkte und ihre Achse.
- Konstruiere nur mit dem Lineal den Bildpunkt eines beliebigen
Punktes Q.
- Konstruiere das Bild einer Geraden nur mit dem Lineal. Begründe
deine Konstruktion.
- Zeige: Sind in zwei rechtwinkligen Dreiecken die Hypothenusen und die
Höhen gleich lang, so sind die Dreiecke kongruent.
Definition 4.1.1
Ist ein Viereck achsensymmetrisch an einer Diagonalen, so heißt das Viereck
Drachenviereck oder Drache.
- Konstruiere einen Drachen, von dem gegeben sind:
- [AB] ist 3cm, [BC] 4cm und [BD] ist 5cm lang.
- [AB] ist 3.5cm, [AC] 7cm und [BD] ist 5.6cm lang.
- [AC] ist 6.8cm BD 5.2cm und Winkel
DAB = 1000.
- [AC] ist 8cm lang. Winkel
DAB = 840 und Winkel
ABC = 1100.
- Berechne die fehlenden Winkel eines Drachens ABCD, wenn gegeben
sind:
- Winkel
DAB = 860.
- Winkel
ABC = 1100.
- Winkel
DAB = 980.
- Winkel
BCD = 640.
- Zeige: Ist ein Drache ein Prallelogramm so ist er schon eine Raute.
Eine Raute ist ein Viereck in dem alle vier Seiten gleich lang sind.
- Zeige: Hat ein Kreis um M mit einer Geraden g genau einen
Schnittpunkt F, so steht MF senkrecht auf g. In diesem Fall heisst
die Gerade g Tangente an den Kreis.
- Gegeben ist ein Kreis um M mit Radius r. Konstruiere von einem
Punkt außerhalb des Kreises Tangenten an den Kreis.
- Max soll in der Skizze von A nach B laufen und unterwegs in einem
Punkt C die Wand berühren. Konstruiere den Punkt der Wand, so dass der
Weg von Max möglichst kurz ist.
- Gegeben ist ein spitzer Winkel mit den Schenkeln g und h. Außerdem ist ein
Punkt C im Winkelfeld gegeben. Konstruiere einen Punkt A auf g und einen
Punkt B auf h, so dass das Dreieck ABC möglichst kleinen Umfang hat.
- Im Innern eines Winkel
 (g, h) sind zwei verschiedene
Punkte. Konstruiere einen Punkt C auf D und einen Punkt Q auf h, so
dass das Viereck ABCD minimalen Umfang hat. Wann existiert ein solches
Viereck?
(g, h) sind zwei verschiedene
Punkte. Konstruiere einen Punkt C auf D und einen Punkt Q auf h, so
dass das Viereck ABCD minimalen Umfang hat. Wann existiert ein solches
Viereck?
- (schwer! Das Problem von Fagano:[QS86, Seite 21]).
Einem spitzwinkligen DReieck soll ein Dreieck mit minimalem Umfang
einbeschrieben werden. Zeige: Diese DReieck ist das Höhenfusspunktdreieck.
- Das Rechteck ABCD stellt einen Billardtisch mit den Banden [AB],
[BC], [CD] und [DA] dar. Die Punkte P und Q sind
Billardkugeln. Die Kugel P soll so gestoßen werden, dass sie nach
zweimaliger Reflexion an den Banden die Kugel Q trifft. Konstruiere die
Bahn der Kugel.
Abbildung 4.1:
Billard
 |
Andreas Bartholome
2003-11-28
![]()
