Konstruiere ein Dreieck aus zwei Seiten und einem anliegenden Winkel. Etwa aus
a, b und 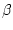 . Diesmal sind zwei Fälle zu unterscheiden.
. Diesmal sind zwei Fälle zu unterscheiden.
- Fall a > b : Der gegebene Winkel liegt der kleineren Seite
gegenüber. Etwa a = 7.5 cm, b = 4.7 cm und
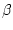 = 340. Führst du die
Konstruktion durch, so siehst du, das es zwei Lösungen gibt.
= 340. Führst du die
Konstruktion durch, so siehst du, das es zwei Lösungen gibt.
- Fall a < b : Der gegebene Winkel liegt der größeren Seit
gegenüber. Beispiel:
a = 5 cm, b = 8, 5 cm und
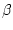 = 800. Führst du diesmal die Konstruktion
durch, so siehst du, das es nur eine Lösung gibt.
= 800. Führst du diesmal die Konstruktion
durch, so siehst du, das es nur eine Lösung gibt.
Dies lässt den folgenden Satz vermuten:
Satz 3.2.4 (SsW)
Zwei Dreiecke, die in zwei Seiten und dem der größeren Seite
gegenüberliegenden Winkel übereinstimmen sind kongruent.
Abbildung 3.4:
SsW
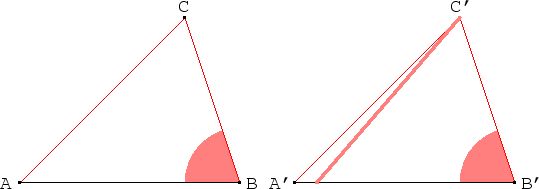 |
Beweis:Seien
 ABC und
ABC und
 A'B'C' zwei DReiecke in denen die
geforderten Stücke gleich sind. Von B' tragen wir auf der Halbgeraden
A'B'] die Strecke c ab und erhalten einen Punkt P. Nach dem Satz SWS
ist
A'B'C' zwei DReiecke in denen die
geforderten Stücke gleich sind. Von B' tragen wir auf der Halbgeraden
A'B'] die Strecke c ab und erhalten einen Punkt P. Nach dem Satz SWS
ist
 C'B'P
C'B'P 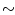
 CBA. Also ist
CBA. Also ist
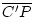 =
= 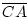 = b. Wäre P echt zwischen A'B', so wäre
nach der vorherigen Folgerung
= b. Wäre P echt zwischen A'B', so wäre
nach der vorherigen Folgerung
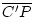 <
< 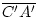 = b. Das ist
nicht der Fall. Genausowenig ist A' zwischen P und B'. Daraus ergibt
sich die Behauptung.
= b. Das ist
nicht der Fall. Genausowenig ist A' zwischen P und B'. Daraus ergibt
sich die Behauptung. 
- Konstruiere ein Dreieck aus:
- a = 5, 3 cm, c = 3, 9 cm und
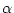 = 400.
= 400.
- a = 3, 8 cm, c = 4, 6 cm und
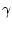 = 720.
= 720.
- b = 4, 7 cm c = 4, 2 cm und
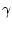 = 400.
= 400.
- b = 6 cm, c = 4, 5 cm und
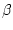 = 1200.
= 1200.
Wie groß ist in jedem Fall die Anzahl der Lösungen?
- Zeige: In jedem rechtwinkligen DReieck liegt der rechte Winkel stets
der größten Seite gegenüber. Diese Seite heißt Hypotenuse.
- Der Punkt P liege nicht auf der Geraden g. Die kürzeste Verbindung
von P zur Geraden ist das Lot auf die Gerade.
- Gegeben ist ein DReieck
 ABC. Das Lot von C auf die
gegenüberliegende Seite [AB] heißt Höhe hc. Entsprechend erklärt man
die anderen Höhen.
Konstruiere in einem Dreieck eigener Wahl alle drei Höhen, was stellst du
fest?
ABC. Das Lot von C auf die
gegenüberliegende Seite [AB] heißt Höhe hc. Entsprechend erklärt man
die anderen Höhen.
Konstruiere in einem Dreieck eigener Wahl alle drei Höhen, was stellst du
fest?
- Konstruiere ein Dreieck aus:
- hc = 5 cm, a = 5, 3 cm und c = 6, 6 cm.
- ha = 6, 3 cm, b = 7cm und c = 6, 5 cm.
- hc = 4, 8 cm, b = 6, 5 cm und
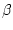 = 700.
= 700.
- hc = 5 cm, b = 5, 3 cm und
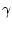 = 600.
= 600.
- Gegeben ist ein Dreieck
 ABC. Zeige:
ABC. Zeige:
- Ist a = b, so ist
ha = hb.
- Ist
ha = hb, so ist a = b.
- Konstruiere ein Dreieck aus:
- b = 4, 6 cm, hc = 4 cm und sb = 6 cm. sb ist die
Seitenhalbierende der Seite b.
- c = 6, 5 cm, sc = 5, 2 cm und hb = 4, 5 cm.
- hc = 4 cm, sc = 5, 2 cm und c = 6, 8 cm.
- c = 7 cm, sb = 6, 6 cm und b = 4, 2 cm.
- c = 8, 8 cm, sc = 2, 9 cm und
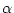 = 280.
= 280.
- Zeige:
- Jeder Punkt der Winkelhalbierenden hat von beiden Schenkeln des
Winkels gleichen Abstand.
- Hat ein Punkt P im Winkelfeld eines Winkels von beiden Schenkeln
geichen Abstand, so liegt er auf der Winkelhalbierenden.
- In jedem Dreieck schneiden sich die Winkelhalbierenden in einem
Punkt. Dieser Punkt ist der Mittelpunkt eines Kreises durch die drei
Fußpunkte der Lote vom Schnittpunkt der Winkelhalbierenden auf die
Seiten. Dieser Kreis heißt Inkreis des Dreiecks.
Andreas Bartholome
2003-11-28