Wir entnehmen der Anschauung folgendes:
Gegeben sei eine Gerade g und ein Punkt A, der nicht auf der Geraden liegt.
Dadurch wird die Ebene in drei Mengen unterteilt.
- Die Halbebene auf der Seite von A.
- Die Halbebene auf der A nicht liegt.
- g selber.
Liegt ein Punkt B nicht in der Halbebene von A, so hat die Strecke [AB]
mit der Geraden g einen Schnittpunkt.
Liegt B in der Halbebene von A, so hat die Strecke [A, B] mit g
keinen Schnittpunkt.
Satz 3.2.1
In jedem Dreieck gilt:
a < b genau dann, wenn
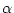 <
< 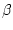 .
Der größeren Seite liegt der größere Winkel gegenüber.
.
Der größeren Seite liegt der größere Winkel gegenüber.
Beweis:Sei zunächst a < b. Dann liegt C auf der Seite von B. Die
Mittelsenkrechte mc von [AB] hat also einen Schnittpunkt S mit
der Geraden CA. Also ist
 SAB =
SAB =  SBA, da das Dreieck
SBA, da das Dreieck
 ABS gleichschenklig ist. Nun ist
ABS gleichschenklig ist. Nun ist
 CAB =
CAB =  SAB <
SAB <  SBA +
SBA +  SBC =
SBC =  CBA. Dies war zu zeigen.
CBA. Dies war zu zeigen.
Es sei
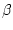 >
> 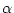 . Wäre a > b, so wäre
. Wäre a > b, so wäre
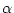 >
> 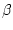 nach der
vorhergehenden Überlegung. Wäre a = b, so wäre
nach der
vorhergehenden Überlegung. Wäre a = b, so wäre
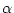 =
= 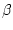 , da in
einem gleichschenkligen Dreieck die Basiswinkel gleich groß sind.
Beides kann nach Voraussetzung nicht sein.
, da in
einem gleichschenkligen Dreieck die Basiswinkel gleich groß sind.
Beides kann nach Voraussetzung nicht sein. 
Folgerung 3.2.2
Ein Dreieck ist genau dann gleichschenklig, wenn die Basiswinkel gleich
groß sind.
Beweis:Ist das Dreieck gleichschenklig, so sind die Basiswinkel gleich groß.
Dies haben wir früher schon in einer Aufgabe gezeigt.
Seien nun die Basiswinkel gleich groß. Dann kann weder a < b noch a > b
gelten, wegen dem Satz vorher. 
Folgerung 3.2.3
In einem Dreieck sei b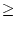 a und P
a und P 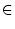 [AB] kein Randpunkt.
Dann ist
[AB] kein Randpunkt.
Dann ist
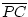 < b.
< b.
Beweis:
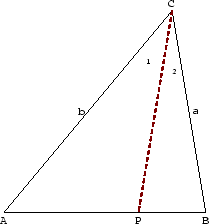
Abbildung 3.3:
Innere Linie
 |
Es ist
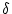 =
= 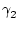 +
+ 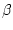 >
> 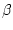 >
> 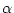 .
Also ist
.
Also ist
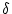 >
> 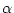 . Daher
b >
. Daher
b > 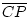

Unterabschnitte
Andreas Bartholome
2003-11-28
![]() SAB =
SAB = ![]() SBA, da das Dreieck
SBA, da das Dreieck
![]() ABS gleichschenklig ist. Nun ist
ABS gleichschenklig ist. Nun ist
![]() CAB =
CAB = ![]() SAB <
SAB < ![]() SBA +
SBA + ![]() SBC =
SBC = ![]() CBA. Dies war zu zeigen.
CBA. Dies war zu zeigen.
![]() >
> ![]() . Wäre a > b, so wäre
. Wäre a > b, so wäre
![]() >
> ![]() nach der
vorhergehenden Überlegung. Wäre a = b, so wäre
nach der
vorhergehenden Überlegung. Wäre a = b, so wäre
![]() =
= ![]() , da in
einem gleichschenkligen Dreieck die Basiswinkel gleich groß sind.
Beides kann nach Voraussetzung nicht sein.
, da in
einem gleichschenkligen Dreieck die Basiswinkel gleich groß sind.
Beides kann nach Voraussetzung nicht sein. ![]()
![]()