Winkel an Doppelkreuzungen
Zwei Geraden heißen parallel , wenn sie ein gemeinsames Lot
haben.
Es sei eine Doppelkreuzung gegeben (siehe Zeichnung). Die Winkel
alpha und alpha'
heißen Stufenwinkel.
Die Winkel
delta und alpha'
heißen Nachbarwinkel.
Die Winkel gamma und alpha'
heißen Z- Winkel oder Wechselwinkel.
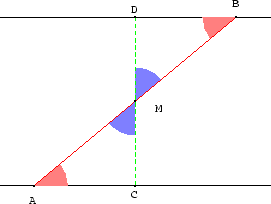
Abbildung 2.2:
Doppelkreuzung
 |
Satz 2.2.1
Die beiden Geraden g und h werden von einer dritten Geraden i
geschnitten. Dann gilt:
- Sind Z- Winkel gleich groß, so sind die Geraden parallel.
- Sind Stufenwinkel gleich groß, so sind die Geraden parallel.
- Ergänzen sich die Nachbarwinkel zu 1800, so sind die
Geraden parallel.
Beweis:Sei M der Mittelpunkt von [A, B] und l das Lot von M auf g.
Dann sind die Dreiecke
 ACM und
ACM und
 BDM kongruent.
Es ist
BDM kongruent.
Es ist
 MBD =
MBD =  MAC nach Voraussetzung.
MAC nach Voraussetzung.
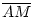 =
= 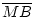 nach Voraussetzung.
nach Voraussetzung.
 CMA =
CMA =  BMD (Scheitelwinkel).
Wegen dem Satz WSW sind also die Dreiecke
BMD (Scheitelwinkel).
Wegen dem Satz WSW sind also die Dreiecke
 ACM und
ACM und
 BDM
kongruent. Das ergibt
BDM
kongruent. Das ergibt
 BDM = 900 und nach Definition sind die
Geraden g und h parallel.
BDM = 900 und nach Definition sind die
Geraden g und h parallel.
Zu 2.
Seien in der Zeichnung die Stufenwinkel
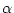 =
= 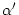 . Es ist
. Es ist
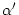 =
= 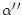 , weil dies Scheitelwinkel sind. Daher ist
, weil dies Scheitelwinkel sind. Daher ist
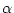 =
= 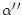 .
Wegen dem bewiesenen Teil 1. des Satzes können wir schließen, dass g und h
parallel sind.
.
Wegen dem bewiesenen Teil 1. des Satzes können wir schließen, dass g und h
parallel sind. 
Beweise die Behauptung 3. selbstständig als Übung.
Ist eine Gerade g gegeben und ein Punkt P außerhalb dieser Geraden, so ist
es leicht eine Parallele zu dieser Geraden durch den Punkt P zu
zeichnen. Wir fällen das Lot von P auf g und errichten in P die
Senkrechte auf dem Lot. Dies ist die gesuchte Parallele. Max schlägt eine
andere Konstruktion vor.
- Wähle irgend einen Punkt Q
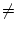 P, welcher nicht auf g liegt.
P, welcher nicht auf g liegt.
- Fälle von Q aus das Lot l auf g.
- Von P aus fälle das Lot h auf l.
Die Gerade h ist eine Parallele durch P zu g. Denn l ist ein
gemeinsames Lot.
Es gibt keinen vernünftigen Grund Max zu widersprechen. Er hat tatsächlich
recht. Führen wir die Konstruktion durch, so sehen wir: Maxens Parallele und
unsere liegen aufeinander. Sind sie gleich oder liegt es an unserer
mangelnden Zeichengenauigkeit? Euklid und mit ihm die meisten Mathematiker
meinten: Sie sind gleich. Über 2000 Jahre lang hat man versucht, dies zu
beweisen. Schon Euklid hat vergeblich versucht dies auf die anderen Grundlagen
der Geometrie zurückzuführen. Da es ihm nicht gelang nahm er diese
einleuchtende, so selbstverständliche Tatsache als
weiteren Grundsatz, Fundamentstein zu seinem Lehrgebäude hinzu. Er formulierte
als Axiom:
Axiom 2..1 (Parallelenaxiom von Euklid)
Ist P ein Punkt, der nicht auf der Geraden g liegt, so gibt es
genau eine Parallele durch P zu g.
Mit diesem Axiom können wir die umgekehrte Frage beantworten: Sind an
parallelen Geraden Wechselwinkel und Stufenwinkel gleich groß?
Satz 2.2.2
Sei g parallel zu h und i schneide g und h.
Dann gilt:
- Z- Winkel sind gleich groß.
- Stufenwinkel sind gleich groß.
- Nachbarwinkel ergänzen sich zu 1800.
Beweis:
Trage in B an i den Winkel 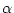 an. Nenne diese Gerade h'.
h' ist parallel zu g nach dem Satz vorher.
Da es nur eine Parallele zu g durch B gibt ist h' = h.
Beweise den Rest selbstständig.
an. Nenne diese Gerade h'.
h' ist parallel zu g nach dem Satz vorher.
Da es nur eine Parallele zu g durch B gibt ist h' = h.
Beweise den Rest selbstständig. 
Folgerung 2.2.3
- Sind g und h parallel und ist i eine Senkrechte zu g, dann ist i
auch senkrecht auf h.
- Seien g und h parallel. Weiter seien A, B Punkte auf
g. Die Lote von A auf h und B auf h sind gleichlang.
- g und h seien zwei Geraden. Gibt es Punkte A und B auf g
derart, dass die Lote von A und B auf h gleichlang
sind, so ist g parallel zu h.
Beweis:
Es ist 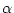 ein Z- Winkel zu
ein Z- Winkel zu 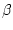 und da
und da
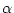 = 900 ist, gilt
dasselbe für
= 900 ist, gilt
dasselbe für 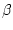 .
.
Zu 2.
D und C sind die Fußpunkte der Lote von A beziehungsweise
B auf h. Da h eine gemeinsame Senkrechte von AD und BC ist, sind
AD und BC parallel. Also gilt:
 BAC =
BAC =  DCA (Z- Winkel).
DCA (Z- Winkel).
 DAC =
DAC =  BCA (Z- Winkel, da AD parallel zu BC).
BCA (Z- Winkel, da AD parallel zu BC).
Die Strecke [AC] haben die Dreiecke
 ADC und
ADC und
 CBA gemeinsam.
Also ist nach dem Satz (WSW)
CBA gemeinsam.
Also ist nach dem Satz (WSW)
 ADC
ADC 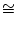
 CBA.
Daher ist
CBA.
Daher ist
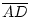 =
= 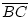 .
.
Zu 3.
Wieder ist AD parallel zu BC wegen der gemeinsamen Senkrechten h.
Also gilt:
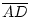 =
= 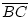 wegen der Voraussetzung.
wegen der Voraussetzung.
 DAC =
DAC =  BCA (Z- Winkel).
Die Strecke [AC] ist den Dreiecken
BCA (Z- Winkel).
Die Strecke [AC] ist den Dreiecken
 ADC und
ADC und
 CBA gemeinsam.
Wegen dem Satz (SWS) ist damit das Dreieck
CBA gemeinsam.
Wegen dem Satz (SWS) ist damit das Dreieck
 CBA
kongruent zum Dreieck
CBA
kongruent zum Dreieck
 ADC.
ADC.
Also ist
 ACD =
ACD =  CAB
und damit sind g und h parallel.
CAB
und damit sind g und h parallel. 
Unterabschnitte
Andreas Bartholome
2003-11-28
![]() =
= ![]() . Es ist
. Es ist
![]() =
= ![]() , weil dies Scheitelwinkel sind. Daher ist
, weil dies Scheitelwinkel sind. Daher ist
![]() =
= ![]() .
Wegen dem bewiesenen Teil 1. des Satzes können wir schließen, dass g und h
parallel sind.
.
Wegen dem bewiesenen Teil 1. des Satzes können wir schließen, dass g und h
parallel sind. ![]()
![]() an. Nenne diese Gerade h'.
h' ist parallel zu g nach dem Satz vorher.
Da es nur eine Parallele zu g durch B gibt ist h' = h.
Beweise den Rest selbstständig.
an. Nenne diese Gerade h'.
h' ist parallel zu g nach dem Satz vorher.
Da es nur eine Parallele zu g durch B gibt ist h' = h.
Beweise den Rest selbstständig. ![]()
![]() ein Z- Winkel zu
ein Z- Winkel zu ![]() und da
und da
![]() = 900 ist, gilt
dasselbe für
= 900 ist, gilt
dasselbe für ![]() .
.
![]() BAC =
BAC = ![]() DCA (Z- Winkel).
DCA (Z- Winkel).
![]() DAC =
DAC = ![]() BCA (Z- Winkel, da AD parallel zu BC).
BCA (Z- Winkel, da AD parallel zu BC).
![]() ADC und
ADC und
![]() CBA gemeinsam.
Also ist nach dem Satz (WSW)
CBA gemeinsam.
Also ist nach dem Satz (WSW)
![]() ADC
ADC ![]()
![]() CBA.
Daher ist
CBA.
Daher ist
![]() =
= ![]() .
.
![]() =
= ![]() wegen der Voraussetzung.
wegen der Voraussetzung.
![]() DAC =
DAC = ![]() BCA (Z- Winkel).
Die Strecke [AC] ist den Dreiecken
BCA (Z- Winkel).
Die Strecke [AC] ist den Dreiecken
![]() ADC und
ADC und
![]() CBA gemeinsam.
Wegen dem Satz (SWS) ist damit das Dreieck
CBA gemeinsam.
Wegen dem Satz (SWS) ist damit das Dreieck
![]() CBA
kongruent zum Dreieck
CBA
kongruent zum Dreieck
![]() ADC.
ADC.
![]() ACD =
ACD = ![]() CAB
und damit sind g und h parallel.
CAB
und damit sind g und h parallel. ![]()