Gegeben ist ein Punkt P auf der Geraden g. Konstruiere eine
Gerade durch P, die senkrecht auf g steht. Man sagt:
Errichte auf g in P die Senkrechte.
Lösung:
- Zeichne k(P, r) mit beliebigem r. Die Schnittpunkte des Kreises
mit der Geraden seien A, B.
- Errichte auf [AB] die Mittelsenkrechte m[AB].
Denken wir noch einmal über die Konstruktion der Mittelsenkrechten einer
Strecke [AB] nach. Entscheidend waren doch zwei Punkte C und D, die
jeweils von A und B gleichweit entfernt sind.
Die Verbindungsstrecke [CD] ist dann die gesuchte Mittelsenkrechte.
Dabei waren D und C völlig beliebig. Das heißt doch: Jeder Punkt, welcher
von A und B gleich weit entfernt ist, liegt auf der Mittelsenkrechten.
Die Mittelsenkrechte m einer Strecke [AB] teilt die Ebene in zwei Hälften.
Eine Hälfte, in der A liegt und eine Hälfte, in der B liegt. Verbindet man
einen Punkt aus der Hälfte von B mit A so schneidet diese
Vrebindungsstrecke die Mittelsenkrechte.
Satz 1.3.1
Sei m die Mittelsenkrechte von [AB]. Dann gilt:
- Liegt C auf m, so ist C von A und B gleichweit entfernt.
- Liegt C nicht auf m, so ist C näher an dem Punkt, auf dessen
Seite C liegt.
- Ist
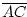 =
= 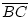 , so liegt C auf m.
, so liegt C auf m.
Beweis:Zu 1. Führe den Beweis selbstständig durch
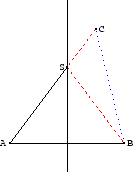
Zu 2.
Es ist nach der Zeichnung
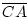 =
= 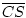 +
+ 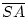 +
+ 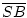 (nach Teil 1.) >
(nach Teil 1.) > 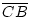 .
Dies gilt, da die Gerade die kürzeste Verbindung zweier Punkte ist.
Genauso ist der Beweis zu führen, wenn C auf der Seite von A liegt.
.
Dies gilt, da die Gerade die kürzeste Verbindung zweier Punkte ist.
Genauso ist der Beweis zu führen, wenn C auf der Seite von A liegt.
Zu 3. Läge C nicht auf m, so läge C auf der Seite von A oder
auf der Seite von B. Dann wäre entweder
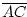 <
< 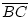 oder
oder
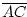 >
> 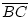 . Beides kann nach Voraussetzung nicht sein.
. Beides kann nach Voraussetzung nicht sein. 
Satz 1.3.2
Die Mittelsenkrechten der drei Seiten eines jeden Dreiecks
 ABC
schneiden sich in einem Punkt.
ABC
schneiden sich in einem Punkt.
Beweis:Sei M der Schnittpunkt von mc und ma. Dann ist
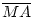 =
= 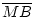 und
und
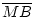 =
= 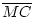 .
Also ist
.
Also ist
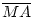 =
= 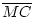 . Damit liegt M auch auf der
Mittelsenkrechten mb.
. Damit liegt M auch auf der
Mittelsenkrechten mb. 
Abbildung 1.1:
Umkreis
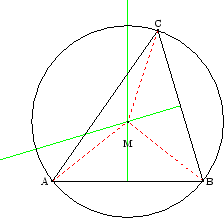 |
Folgerung 1.3.3
Der Schnittpunkt der Mittelsenkrechten eines Dreiecks ist der Mittelpunkt eines
Kreises, auf dem die drei Eckpunkte des Dreiecks liegen.
Dieser Kreis heißt Umkreis des Dreiecks.
Andreas Bartholome
2003-11-28
![]() =
= ![]() +
+ ![]() +
+ ![]() (nach Teil 1.) >
(nach Teil 1.) > ![]() .
Dies gilt, da die Gerade die kürzeste Verbindung zweier Punkte ist.
Genauso ist der Beweis zu führen, wenn C auf der Seite von A liegt.
.
Dies gilt, da die Gerade die kürzeste Verbindung zweier Punkte ist.
Genauso ist der Beweis zu führen, wenn C auf der Seite von A liegt.
![]() <
< ![]() oder
oder
![]() >
> ![]() . Beides kann nach Voraussetzung nicht sein.
. Beides kann nach Voraussetzung nicht sein. ![]()