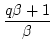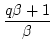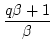Kettenbrüche
Wir betrachten noch einmal die Divisionsgleichung zu einem gegebenem
Zahlenpaar
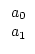
 . Wegen Satz 3.1 gibt es eindeutig
bestimmte Zahlen
q0
. Wegen Satz 3.1 gibt es eindeutig
bestimmte Zahlen
q0 
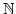 und
a2
und
a2 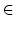
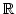 + mit
+ mit
Es ist
q0 = [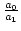 ].
Zu jedem Paar
].
Zu jedem Paar
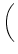
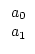
 gehört also eine Quotientenfolge eine
Folge
(qn| n
gehört also eine Quotientenfolge eine
Folge
(qn| n 
 ) mit qi > 0, die durch das euklidische Verfahren
definiert ist.
So ist
) mit qi > 0, die durch das euklidische Verfahren
definiert ist.
So ist
116 = 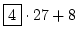 |
oder |
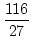 = = 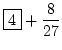 |
|
27 = 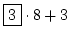 |
oder |
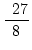 = = 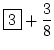 |
|
8 = 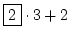 |
oder |
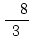 = = 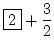 |
|
3 = 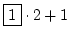 |
oder |
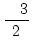 = = 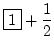 |
|
2 = 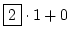 |
oder |
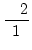 = = 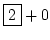 |
|
In diesem Beispiel ist die entstehende Zahlenfolge endlich.
Setzt man ein so erhält man:
Es entsteht in unserm Beispiel ein endlicher Kettenbruch. Die Schreibweise ist
sehr unbequem. Da es nur auf die Quotienten ankommt schreibt man in unserm
Beispiel:
[4, 3, 2, 1, 2]. Man kann nun endliche Kettenbrüche rekursiv definieren:
- Für jede natürliche Zahl q0 ist
[q0] : = q0.
- Es ist
[q0, q1,..., qn+1] : = q0 +
![$\displaystyle {\frac{{1}}{{[q_{1},\dots,q_{n+1}]}}}$](img187.png)
Das heißt es ist
[1, 2, 3] = 1 + ![$\displaystyle {\frac{{1}}{{[2,3]}}}$](img188.png) = 1 +
= 1 + 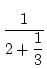 .
Startet man den euklidischen Algorithmus mit zwei inkommensurablen Zahlen, so
bricht er nicht ab, wie wir wissen. Wir wollen beispielsweise die
Quotientenfolge für das Zahlenpaar
.
Startet man den euklidischen Algorithmus mit zwei inkommensurablen Zahlen, so
bricht er nicht ab, wie wir wissen. Wir wollen beispielsweise die
Quotientenfolge für das Zahlenpaar
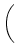
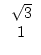
 berechnen. Es muss
sich auf jeden Fall eine unendliche Folge ergeben.
Es entsteht im euklidischen Algorithmus eine Zahlenfolge
berechnen. Es muss
sich auf jeden Fall eine unendliche Folge ergeben.
Es entsteht im euklidischen Algorithmus eine Zahlenfolge
| an |
= |
qn . an+1 + an+2 |
|
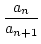 |
= |
qn + 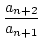 qn qn   |
|
Definiert man
bn : = 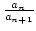 , so gilt:
bn = qn +
, so gilt:
bn = qn + 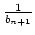 . oder:
. oder:
bn+1 = ![$\displaystyle {\frac{{1}}{{b_{n}-[b_{n}]}}}$](img198.png) |
|
Diese leichte Umformung erleichtert das Berechnen der Quotientenfolge
Beispiele:
- Es soll die Kettenbruchentwicklung von
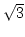 bestimmt werden.
Zur Abkürzung sei
w =
bestimmt werden.
Zur Abkürzung sei
w = 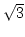 .
.
| b0 = w,[b0] = q0 |
= |
1 |
|
b1 = 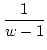 , b1 = , b1 = 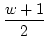 , q1 , q1 |
= |
1 |
|
b2 = 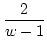 = w + 1, q2 = w + 1, q2 |
= |
2 |
|
b3 = 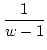 |
= |
b1 |
|
Wie wir sehen wiederholen sich ab jetzt dieselbe bi. Die Quotientenfolge
wird daher periodisch.
Wir kürzen das folgendermaßen ab:
[1,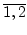 ].
].
- Es soll dei Kettenbruchentwicklung von
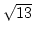 berechnet werden.
w =
berechnet werden.
w = 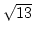
| n |
bn = 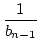 - [bn] - [bn] |
qn = [bn] |
| 0 |
w = 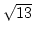 |
3 |
| 1 |
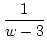 = = 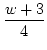 |
![$ \left[\vphantom{\displaystyle\frac{[w]+3}{4}}\right.$](img208.png) ![$\displaystyle {\frac{{[w]+3}}{{4}}}$](img209.png) ![$ \left.\vphantom{\displaystyle\frac{[w]+3}{4}}\right]$](img210.png) = 1 = 1 |
| 2 |
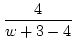 = = 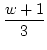 |
1 |
| 3 |
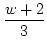 |
1 |
| 4 |
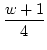 |
1 |
| 5 |
w + 3 |
6 |
| 6 |
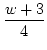 |
1 |
| |
|
|
Wir haben daher
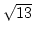 = [3,
= [3,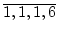 ].
].
Schreibt man diese Gleichung wieder mit dem tollen Hilfsmittel der Matrizen,
so erhält man:
Auf
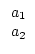
 wenden wir das gleiche Verfahren an:
Es ist
wenden wir das gleiche Verfahren an:
Es ist
| a1 |
= |
q1 . a2 + a3 q1 = 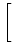 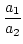 ![$\displaystyle \left.\vphantom{\frac{a_{1}}{a_{2}}}\right]$](img225.png) > 1. > 1. |
|
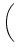 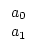  |
= |
A0 . A1 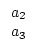  |
|
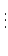 |
= |
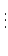 |
|
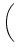 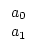  |
= |
  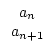 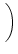 |
(13) |
| |
|
|
|
Hinweise:
- Zu jedem Zahlenpaar
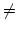
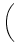
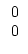
 gehört eigenlich eine Gerade
durch den Ursprung, so dass unsere Matrizen Abbildungen zwischen solchen
Geraden induzieren.
gehört eigenlich eine Gerade
durch den Ursprung, so dass unsere Matrizen Abbildungen zwischen solchen
Geraden induzieren.
- Brüche sind nichts anderes als Zahlenpaare. So konstruiert man auch
Brüche. Von daher liegt es nahe sein Augenmerk auf Zahlenpaare zu lenken.
Aufgaben:
- Gegeben die endliche Quotientenfolge
[5, 4, 3, 2, 2]. Welche Zahlenpaare
gehören zu dieser Quotientenfolge?
- Zeige: Die Quotientenfolge die zu (a, b) gehört ist genau dann endlich,
wenn a und b kommensurabel sind. Dies wusste schon Euklid.
- Bei der Berechnung der Kettenbruchentwicklung einer Quadratwurzel ist
folgende Bemerkung wichtig:
[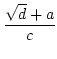 ] = [ ] = [![$\displaystyle {\frac{{[\sqrt{d}]+b}}{{c}}}$](img240.png) ] ] |
(14) |
Falls
a, b, c, d 
 und d keine Quadratzahl ist. Um
[
und d keine Quadratzahl ist. Um
[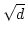 ] zu
berechnen gibt es ein schnelles Verfahren, welches nur mit natürlichen Zahlen
rechnet.
Es ist eine Abwandlung des Newton Verfahrens
[Lün87, Seite 30]
] zu
berechnen gibt es ein schnelles Verfahren, welches nur mit natürlichen Zahlen
rechnet.
Es ist eine Abwandlung des Newton Verfahrens
[Lün87, Seite 30]
- Berechne die Kettenbruchentwicklung von
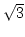 .
.
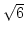 ,
, 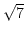 ,
,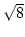 ,
,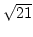
- Finde ein Zahlenpaar zu dem die unendliche Quotientenfolge
[
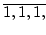 ] gehört.
] gehört.
- Finde ein Zahlenpaar das zu der Quotientenfolge
[2, 2, 2, 2, 2, 2,...]
gehört.
- Berechne die Kettenbruchentwicklung von
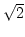 + 1.
+ 1.
- Berechne die Kettenbruchentwicklung von
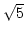 + 2
+ 2
- Berechne allgemein die Kettenbruchentwicklung von
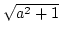 + a
falls a2 + 1 keine Quadratzahl ist.
+ a
falls a2 + 1 keine Quadratzahl ist.
Bemerkung 4.1
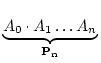
Für
Pn = 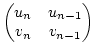 gelten die Rekursionsformeln:
gelten die Rekursionsformeln:
| un+1 |
= |
qn+1 . un + un-1 |
|
| vn+1 |
= |
qn+1 . vn + vn-1 |
(15) |
Die Determinante
det(Pn) = (- 1)n.
vn, un sind streng
monoton wachsende Folgen. (Dies ist genau wie im Satz 2.2)
Beweis:

Folgerung 4.3
- Ist
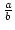 eine irrationale Zahl, so ist
eine irrationale Zahl, so ist
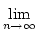
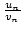 =
= 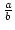
- Zwei Zahlenpaare (a, b) und (c, d ) haben dieselbe Quotientenfolge, wenn
sie auf der gleichen Geraden durch den Nullpunkt liegen.
Beweis:1. ist klar
Zu 2. Liegen die beiden Zahlenpaare (a, b) und (c, d ) auf der gleichen
Geraden durch den Nullpunkt, so sind ihre Quotienten gleich. Sie erzeugen also
die gleiche Quotientenfolge.
Seien umgekehrt die Quotientenfolgen gleich. Man hat für alle natürlichen
Zahlen:
Dabei ist
Pn = 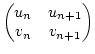 Es folgt
Es folgt
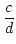 =
= 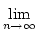
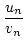 =
= 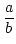 .
Das war behauptet.
.
Das war behauptet. 
Beweis:Zunächst nur für den Fall, dass die Quotientenfolge
[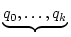 , q0,..., qk...] rein periodisch
ist.
Wir haben dann:
, q0,..., qk...] rein periodisch
ist.
Wir haben dann:
Wobei
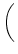
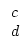
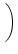 dieselbe Quotientenfolge hat. Es folgt dann:
dieselbe Quotientenfolge hat. Es folgt dann:
Daher ist x Lösung einer quadratischen Gleichung mit ganzahligen
Koeffizienten.
Es bleibt nur noch der Fall zu überlegen, dass die Quotientenfolge nicht rein
periodisch ist.
Dann gilt:
Dabei erzeugt
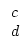
 eine rein periodische Kettenbruchentwicklung.
Mit dem folgenden Hilfssatz ergibt sich die Behauptung.
eine rein periodische Kettenbruchentwicklung.
Mit dem folgenden Hilfssatz ergibt sich die Behauptung.
Hilfssatz 4.5
Sei y eine quadratische Irrationalität. Dann ist
x = 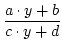 |
(16) |
mit
a, b, c, d 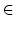
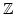 eine quadratische Irrationalität.
eine quadratische Irrationalität.
Beweis:y erfülle die Gleichung
A . y2 + B . y + C = 0. Wir lösen die Gleichung
16 nach y auf. Das ergibt:
y = 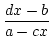 . Setzt man dies in die quadratische
Gleichung ein, die y erfüllt und multipliziert mit dem Hauptnenner, so
sieht man, dass x eine quadrtische Gleichung mit ganzzahligen Koeffizienten erfüllt.
. Setzt man dies in die quadratische
Gleichung ein, die y erfüllt und multipliziert mit dem Hauptnenner, so
sieht man, dass x eine quadrtische Gleichung mit ganzzahligen Koeffizienten erfüllt.


Hinweise:
- Ich habe aus dem Buch von Koch [Koc97, Seite 272] übernommen, dass
der Satz von Euler stammt. Ich weiss aber nicht wo es bei Euler steht.
Satz 4.6
Sei
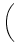
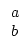
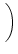 = Pn .
= Pn . 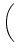
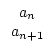
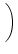 mit Matrizen
der Form
Pn =
mit Matrizen
der Form
Pn = 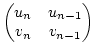 . Ist
. Ist
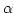 =
= 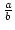 Lösung einer Gleichung
Ax2 + Bx + C = 0 mit ganzzahligen Koeffizienten, so ist
Lösung einer Gleichung
Ax2 + Bx + C = 0 mit ganzzahligen Koeffizienten, so ist
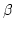 =
= 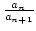 auch Lösung einer Gleichung
Anx2 + Bnx + Cn = 0
mit ganzzahligen Koeffizienten und gleicher Determinante.
auch Lösung einer Gleichung
Anx2 + Bnx + Cn = 0
mit ganzzahligen Koeffizienten und gleicher Determinante.
Beweis:Es genügt die Beziehung zu zeigen für eine Beziehung der Form:
Ist
A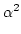 + B
+ B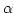 + C = 0, so ist
A
+ C = 0, so ist
A
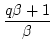
 + B
+ B
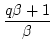
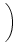 + C = 0
Dies ergibt
+ C = 0
Dies ergibt
(
Aq2 +
Bq +
C)
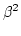
+ (
A2
q +
B)
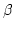
+
A = 0.
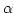 .
. 
Satz 4.7 (Lagrange)
ist a eine quadratische Irrationalität, so defieniert das Zahlenpaar
(a, 1) eine periodische Quotientenfolge. Der Kettenruch ist periodisch.
Hinweise:
- Der Zusammenhang mit den gebrochen rationalen Funktionen
fehlt. Eindimensionaler projektiver Raum.
- Wir sollten die Originalschrift von Luca Pcioli finden.
- Auch das Liber abaci von Leonardo von Pisa.
- Außerdem die Schrift von Lagrange.
- In der Musik spielt der goldene Schnitt und die Fibonacci Zahlen auch
eine große Rolle. Besonders bei Bela Bartok siehe das Buch [Sza72, Seite 105 ff]
Andreas Bartholome
2004-10-27
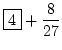
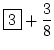
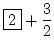
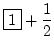
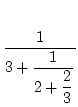 = 4 +
= 4 + 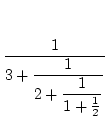
![$\displaystyle {\frac{{1}}{{[q_{1},\dots,q_{n+1}]}}}$](img187.png)
![$\displaystyle {\frac{{1}}{{b_{n}-[b_{n}]}}}$](img198.png)
![$\displaystyle {\frac{{[w]+3}}{{4}}}$](img209.png)
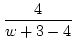 =
= 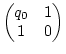
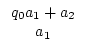
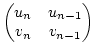 gelten die Rekursionsformeln:
gelten die Rekursionsformeln:
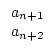
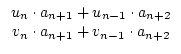
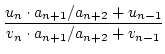
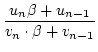 mit
mit 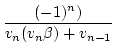
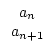
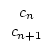
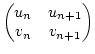 Es folgt
Es folgt
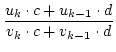
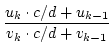
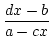 . Setzt man dies in die quadratische
Gleichung ein, die y erfüllt und multipliziert mit dem Hauptnenner, so
sieht man, dass x eine quadrtische Gleichung mit ganzzahligen Koeffizienten erfüllt.
. Setzt man dies in die quadratische
Gleichung ein, die y erfüllt und multipliziert mit dem Hauptnenner, so
sieht man, dass x eine quadrtische Gleichung mit ganzzahligen Koeffizienten erfüllt.
![]()
![]()
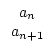
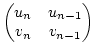 . Ist
. Ist
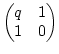
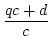 =
= 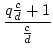 =
=