- Sei c > 0. a0 : = c und
an+1 : =
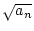 . Zeigen Sie
die Folge konvergiert. Berechnen Sie den Grenzwert.
. Zeigen Sie
die Folge konvergiert. Berechnen Sie den Grenzwert.
- Zeige die Folge
- Sei in der logistischen Gleichung 1.7
sei r = 1.9. Wähle als Startwert a0 : = 0.1.
- Zeige: Die Folge ist konvergent.
- Berechne den Grenzwert der Folge.
- Sei r = 2.1. Beantworte mit diesem Parameter
die gleichen Fragen wie in der Aufgabe vorher.
- Sei
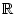
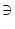 a > 1.
a0 : = a und
an+1 : =
a > 1.
a0 : = a und
an+1 : = 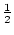 . (an +
. (an + 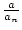 ).
Zeige die Folge konvergiert. Berechne den Grenzwert.
).
Zeige die Folge konvergiert. Berechne den Grenzwert.
- Gegeben sind die Folgen durch Rekursion:
Beweise, dass die Folgen konvergieren und berechnen Sie den Grenzwert.
- a0 : = 0,
an+1 : =
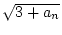 .
.
- a0 : = 0,
an+1 : =
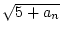 .
.
- a0 : = 2,
an+1 : =
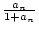 .
.
- Genügt ein Turm von endlicher Höhe, damit sein Lift aus 10m Höhe
wieder um die Hälfte dieser Höhe abwärts, dann um 40m aufwärts,
dann um die Hälte dieser Höhe abwärts, dann wieder um 40m
aufwärts fahren kann usw. ?
- Für zwei positive Zahlen a, b definieren wir die Folgen
(an) und (bn) folgendermaßen.
a0 : =
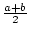 .
b0 : =
.
b0 : = 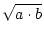 an+1 : =
an+1 : = 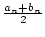 bn+1 : =
bn+1 : = 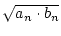 .
Man beweise, dass beide Folgen den selben Grenzwert haben.
Das sogenannte ,,arthmetische geometrische Mittel``.
.
Man beweise, dass beide Folgen den selben Grenzwert haben.
Das sogenannte ,,arthmetische geometrische Mittel``.
- Die Folge (an) ist folgendermaßen definiert:
a0 : = 0, a1 : = 1 und
an+1 : = an + an+1.
Dies ist die Fibionacci Folge.
Zeige:
-
an+1 . an-1 - an2 = (- 1)n für alle
n
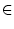
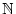
- Zeige: Die Quotientenfolge
bn : =
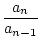 ist konvergent. Welchen Grenzwert hat sie?
ist konvergent. Welchen Grenzwert hat sie?
- Die Folge (an) sei folgendermaßen definiert:
(a0) : = 0.
an+2 : = 2 . an+1 + an. Konvergiert die Folge?
Wenn ja berechne den Grenzwert.
- Die Folge (an) sei folgendermaßen definiert:
(a0) : = 0.
an+2 : = 3 . an+1 + an. Konvergiert die Folge?
Wenn ja berechne den Grenzwert.
- Die Folge (an) sei folgendermaßen definiert:
(a0) : = 0.
an+2 : = b . an+1 + an. Konvergiert die Folge?
Wenn ja berechne den Grenzwert. Dabei ist b irgend eine feste positive
Zahl.
- Wir definieren folgendermaßen induktiv zwei Folgen:
a0 : = 3, b0 : = 2 und
an+1 : = 3 . an +4 . bn,
bn+1 : = 2 . an +3 . bn.
- Berechne die Folgenglieder für möglichst große
n
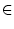
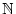 .
.
- Zeigen Sie: Für alle
n
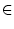
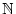 ist
(an)2 -2 . (bn)2 = 1.
ist
(an)2 -2 . (bn)2 = 1.
- Zeigen Sie: Die Folge
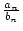 konvergiert.
Berechnen Sie den Grenzwert.
konvergiert.
Berechnen Sie den Grenzwert.
- Zeige: In der Methode von Archimedes ist (Un) eine monoton
wchsende beschränkte Folge.
Andreas Bartholome
2003-11-26