Wir brauchen unbedingt Konvergenzkriterien. Ein einleuchtendes Prinzip
ist folgendes:
Axiom 1..1
Jede monoton wachsende und nach oben beschränkte Folge ist konvergent.
Wir können dies mit unsern Mitteln nicht beweisen. Noch Gauß nahm diese
Tatsache ohne darüber nachzudenken als selbstverständlich an.
Wir tun es auch.
Satz 1.3.1
Äquivalent sind:
- Jede monoton wachsende und nach oben beschränkte Folge ist konvergent.
- Jede monoton fallende und nach unten beschränkte Folge ist
konvergent.
Beweis:1.
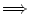 2.
Sei (bn) eine monoton fallende und durch s nach unten beschränkte
Folge.
Dann ist (- bn) nach oben durch (- s) beschränkt und (- bn) ist monoton
wachsend. Also ist (- bn) konvergent. Daher ist
(bn) = (- 1) . (- bn)
auch konvergent.
2.
Sei (bn) eine monoton fallende und durch s nach unten beschränkte
Folge.
Dann ist (- bn) nach oben durch (- s) beschränkt und (- bn) ist monoton
wachsend. Also ist (- bn) konvergent. Daher ist
(bn) = (- 1) . (- bn)
auch konvergent.
2.
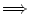 1. Genauso.
1. Genauso. 
Mit diesem Kriterium können wir nun in einigen Fällen entscheiden, wann
unser Itertionsverfahren mit der Gleichung 1.7 konvergiert.
Wir hatten beispielsweise vermutet, dass für r = 1 und beliebigen Startwert
aus [0, 1] die Folge gegen 0 konvergiert. Dies ist tatsächlich richtig.
Denn es ist
an+1 = an . (1 - an) an, da
0
an, da
0 1 - an
1 - an 1
für
an
1
für
an  [0, 1].
Also ist die Folge monoton fallend.
Sie ist sowieso nach unten beschränkt durch
0. Also ist die Folge konvergent. Dann stimmt aber der Grenzwert, den wir
vorher ausgerechnet haben.
[0, 1].
Also ist die Folge monoton fallend.
Sie ist sowieso nach unten beschränkt durch
0. Also ist die Folge konvergent. Dann stimmt aber der Grenzwert, den wir
vorher ausgerechnet haben.
Wie sieht es aus, wenn wir in der logistischen Gleichung 1.7
r = 2 wählen? Wir hatten vermutet, dass dann der Grenzwert 0.5 ist.
Um dies zu beweisen ist es nützlich, den Graphen der Funktion
f (x) = 2 . x . (1 - x) zu betrachten
Die Scheitelform dieser Parabel erhält man durch
f (x) = (- 2) . (x2 - x + 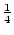 -
- 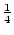 ) = (- 2) . (x -
) = (- 2) . (x - 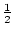 )2 +
)2 + 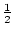 .
Das heißt für
x
.
Das heißt für
x  [0, 1] ist
f (x)
[0, 1] ist
f (x)  [0,
[0,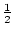 ].
Wählen wir für unsere Folge irgend einen Startwert aus [0, 1],
so ist die Folge auf jeden Fall durch
].
Wählen wir für unsere Folge irgend einen Startwert aus [0, 1],
so ist die Folge auf jeden Fall durch
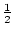 nach oben beschränkt.
Wählen wir als Startwert a0 : = 0.1, so überlegt man sich, dass
an
nach oben beschränkt.
Wählen wir als Startwert a0 : = 0.1, so überlegt man sich, dass
an 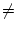 1 für alle
n
1 für alle
n 
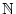 und an
und an 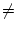 0 für alle
n
0 für alle
n 
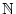 .
Dann gilt aber
an
.
Dann gilt aber
an an+1
an+1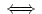 an
an 2 . an . (1 - an)
2 . an . (1 - an)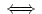 an
an
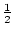 .
Die letzte Ungleichung haben wir schon als richtig erkannt.
Also gilt die erste.
Daher ist (an) monoton wachsend und es ist (an) konvergent.
Beispiele:
.
Die letzte Ungleichung haben wir schon als richtig erkannt.
Also gilt die erste.
Daher ist (an) monoton wachsend und es ist (an) konvergent.
Beispiele:
- Das Heron Verfahren zur Berechnung der Wurzel
Die Griechen haben ein rafiniertes Verfahren entwickelt unm die Wurzel aus
einer positiven Zahl zu berechnen. Wie so oft war die Geometrie der
Ausgangspunkt ihrer Ideeen. Ich möchte die Methode an einem
Beispiel erklären. Es soll
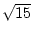 berechnet werden. Wir gehen von
einem Rechteck mit den Seiten a0 : = 5 und b0 : = 3 aus.
berechnet werden. Wir gehen von
einem Rechteck mit den Seiten a0 : = 5 und b0 : = 3 aus.
Abbildung 1.2:
Heron Verfahren
|
![\includegraphics[height=3cm]{/home/andreas/tex/schule/elfte/bild/bilder1}](img156.png) |
Dies ist kein Quadrat. Wir wählen als neue Seitenlängen:
a1 : = 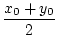 undy1 : = undy1 : = 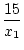 |
|
Macht man weiter so erhällt man:
Allgemein erhält man eine rekursiv definierte Folge mit:
xn+1 : = 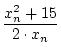 |
|
Bemerkung 1.3.2
Sei
f (x) : = 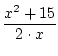 und
M = {x| f (x)
und
M = {x| f (x)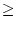 15}
Dann ist
f : M
15}
Dann ist
f : M 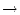 M eine Progression für die Halbordnung
M eine Progression für die Halbordnung 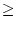 . Das
heißt für alle x
. Das
heißt für alle x  M ist x
M ist x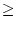 f (x).
f (x).
Man rechnet leicht nach, dass f (x)  M ist für x
M ist für x  M. Außerdem zeigen
zwei Äquivalenzumformungen sofort, dass x
M. Außerdem zeigen
zwei Äquivalenzumformungen sofort, dass x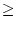 f (x) für alle x
f (x) für alle x  M gilt.
M gilt.
Benutzt man zur Berchnung der Iterationsschritte einen Rechner, der
Langzahlarithmetik beherrscht kann man sehr einfach die Wurzel mit belibeiger
Genauigkeit ausrechnen.
Beispielsweise bc der in jeder Linux Distribution enthalten ist.
scale =10000
a=2
for(i=1;i<=50;i++)
{a=(a*a+2)/(2*a);
}
print a, "\n"
print "Wurzel aus 2:", sqrt(2), "\n"
quit
Hat diese Programm den Namen 3.bc so ruft man es von einer shell aus auf durch
bc 3.bc so ergibt es 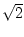 auf 10000 Stellen genau. Die ersten
Stellen sind:
auf 10000 Stellen genau. Die ersten
Stellen sind:
1.41421356237309504880168872420969807856967187537694807317
6679737990732478462107038850387534327641572735013846230912
2970249248360558507372126441214970999358314132226659275055
927557999505011527820605714701
- Berechnung von Pi nach Archimedes:
Abbildung 1.3:
Berechnung der Kreiszahl
|
![\includegraphics[height=5cm]{/home/andreas/tex/schule/elfte/bild/bilder.2}](img164.png) |
s ist die Länge einer Sehne imm Einheitskreis. Sie hat vom Mittelpunkt den
Abstand c. Auf der Sehne errichten wir die Mittelsenkrechte. Diese schneidet
den Einheitskreis in einem Punkt C. Es entsehen zwei neue Sehnen. der Länge
f (s) = x. Die neuen Sehnen haben vom Mittelpunkt den Abstand g(c) = y.
Nach dem Kathetensatz des Euklid gilt
| (2 . y)2 |
= |
(1 + c) . 2 |
|
| y |
= |
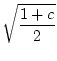 |
|
| g(c) |
= |
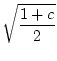 |
(1.7) |
Ist der neue Abstand der kleineren Sehne bekannt, so kann die neue Sehne
berechnet werden. Betrachte man die Zeichnung und berechnet den Flächeninhalt
des Dreiecks
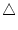 DCB zweimal, so sieht man:
DCB zweimal, so sieht man:
| 2 . y . x |
= |
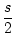 . 2 . 2 |
|
| f (s) |
= |
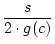 |
(1.8) |
Startet man mit c0 = 0 und definiert induktiv
cn+1 : = 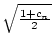 , so erhält man eine Progression.
, so erhält man eine Progression.
Definition 1.3.1
Sei
U 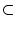
 und
f : U
und
f : U  U. f heisst Progression, wenn
für alle x
U. f heisst Progression, wenn
für alle x  U gilt x
U gilt x f (x). Oder es ist für alle x
f (x). Oder es ist für alle x  U: f (x)
U: f (x) x.
x.
Bemerkung 1.3.3
g : o[0, 1] 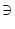 x
x 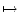 g(c) =
g(c) = 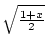 ist eine Progression.
ist eine Progression.
Beweis:Es ist
g(x) = 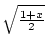 . Dann gelte die Äquivallenzen:
. Dann gelte die Äquivallenzen:
Die letzte Ungleichung ist der Fall. Also ergibt sich die Behauptung. 
Bemerkung 1.3.4
Der Grenzwert der rekursiv definierten Folge c0 : = 0 und
cn+1 : = 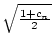 ist 1.
ist 1.
Beweis:Die Folge ist konvergent, da sie monotopn wachsend und nach oben beschränkt
ist. Es ist
cn = 2 . cn+12 - 1. Ist
a = 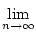 cn, so folgt:
a = 2 . a2 - 1. Darus ergibt sich a = 1.
cn, so folgt:
a = 2 . a2 - 1. Darus ergibt sich a = 1. 
Definiert man passend zu der Abstandsfolge (cn) die Sehnenfolge, und die
Umfangsfolge, so erhält man:
s0 : = 2; und
sn+1 : = 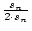 und u0 = 2,
un = 22sn so erhält man eine Annähreung an den Umfang des
Halbkreise. Setzt man weiterhin
tn : =
und u0 = 2,
un = 22sn so erhält man eine Annähreung an den Umfang des
Halbkreise. Setzt man weiterhin
tn : = 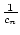 . sn, so ist
On : = 2n . tn der Umfang des n-ten umbeschriebenen regulären
Vielecks.
Dies kann wieder hergenommen werden um mit dem Rechner
bc die
Kreiszahl
. sn, so ist
On : = 2n . tn der Umfang des n-ten umbeschriebenen regulären
Vielecks.
Dies kann wieder hergenommen werden um mit dem Rechner
bc die
Kreiszahl 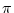 etwa auf 50 Stellen zu berechnen.
etwa auf 50 Stellen zu berechnen.
scale=100
c=0
m=1
for(i=1;i<=50;i++)
{c=sqrt((1+c)/2);
m=2*m;
}
umfang=m*sqrt(4-4*c*c)
print "Anzahl der Ecken: ", m, " Umfang: ",umfang
quit
Es ergibt sich:
Anzahl der Ecken: 1125899906842624 Umfang:
3.141592653589793238462643383278483732551771296666640314903
Unterabschnitte
Andreas Bartholome
2003-11-26
![]() 1. Genauso.
1. Genauso. ![]()
![]() an, da
0
an, da
0![]() 1 - an
1 - an![]() 1
für
an
1
für
an ![]() [0, 1].
Also ist die Folge monoton fallend.
Sie ist sowieso nach unten beschränkt durch
0. Also ist die Folge konvergent. Dann stimmt aber der Grenzwert, den wir
vorher ausgerechnet haben.
[0, 1].
Also ist die Folge monoton fallend.
Sie ist sowieso nach unten beschränkt durch
0. Also ist die Folge konvergent. Dann stimmt aber der Grenzwert, den wir
vorher ausgerechnet haben.
![\includegraphics[height=5cm width=5cm]{/home/andreas/tex/schule/elfte/bild/bild1}](img153.png)
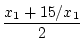 =
= 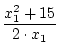
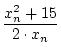
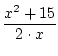 und
M = {x| f (x)
und
M = {x| f (x)