- Beweise durch vollständige Induktion, dass für alle
n
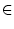
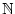 aus
aus
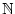 folgende Aussagen gelten.
folgende Aussagen gelten.
-
1 + 2 + 3 +...+ n =
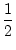 . n . (n + 1).
. n . (n + 1).
-
2 + 4 + 6 +...+2n = n . (n + 1).
-
1 + 3 + 6 +...
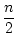 . (n + 1) =
. (n + 1) = 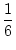 . n . (n + 1) . (n + 2)
. n . (n + 1) . (n + 2)
-
1 . 2 + 2 . 3 +...+ n . (n + 1) =
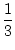 . n . (n + 1) . (n + 2).
. n . (n + 1) . (n + 2).
-
1 . 2 . 3 +...+ n . (n + 1)
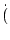 n + 2) =
n + 2) = 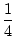 . n . (n + 1) . (n + 2) . (n + 3).
. n . (n + 1) . (n + 2) . (n + 3).
-
12 +22 +32 +...+ n2 =
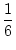 . n . (n + 1) . (2n + 1).
. n . (n + 1) . (2n + 1).
-
12 -22 +32 -42 +...(- 1)n+1*n2 = (- 1)n+1 .
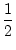 . n . (n + 1).
. n . (n + 1).
-
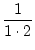 +
+ 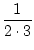 +...+
+...+ 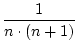 =
= 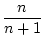 .
.
-
13 +23 +...+ n3 =
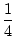 . n2 . (n + 1)2.
. n2 . (n + 1)2.
- Für welche
n
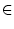
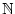 ist 2n
ist 2n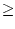 n?
n?
- Für welche
n
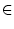
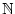 ist 2
ist 2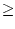 n2?
n2?
- Für welche
n
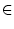
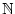 ist
2n > 3n2 + n?
ist
2n > 3n2 + n?
- Für welche
n
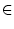
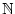 ist 2n + 1 teilbar durch 5 bezw.durch 13?
ist 2n + 1 teilbar durch 5 bezw.durch 13?
- Schreibt man die Zahl 1 n-mal nebeneinander, so
erhält man eine natürliche Zahl. Für welche
n
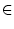
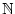 ist diese Zahl durch 13 teilbar?
ist diese Zahl durch 13 teilbar?
- Beweise die sogenannte Bernouillsche Ungleichung:
Für alle h
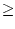 - 1 gilt:
(1 + h)n
- 1 gilt:
(1 + h)n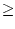 1 + n . h.
1 + n . h.
- Beweise: Für n
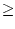 2 und h
2 und h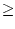 0 gilt:
0 gilt:
(1 +
h)
n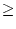
1 +
n . h +
n . (
n - 1)
. 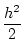
.
- Beweise: Für alle natürlichen Zahlen ist n3 + 5n
durch 6 teilbar.
- n5 - n ist für alle n durch 5 teilbar.
- n7 - n ist für alle n durch 7 teilbar.
- n7 - n ist für alle n durch 42 teilbar.
- Zeige: Für alle
n
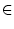
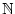 und für alle
a
und für alle
a 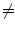 1
1 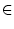
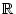 gilt:
gilt:
1 +
a +
a2 +
a3 +
a4...+
an =
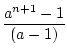
.
- Es gibt eine ganzrationale Funktion 2-ten Grades, die folgende Bedingung
erfüllt.
f (X) + X + 1 = f (X + 1). Leiten Sie daraus die Gaußsche Summenformel
her.
- Es gibt eine ganzrationale Funktion 3-ten Grades, mit:
f (x) + (X + 1)2 = f (X + 1).
Leiten Sie daraus eine Summenformel für die Summe
der ersten n-Quadratzahlen her.
- Es gibt eine ganzrationale Funktion 4-ten Grades
mit
f (X) + (X + 1)3 = f (X + 1). Summenformel für die
ersten n Qubikzahlen.
- Es gibt eine ganzrationale Funktion n + 1-ten
Grades mit:
f (x) + (X + 1)n = f (x + 1). Summenformel für die n-ten
Potenzen!
Andreas Bartholome
2003-11-26
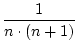 =
= 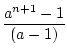 .
.