Nächste Seite: Das Rechnen mit Kongruenzen Aufwärts: Der größte gemeinsame Teiler Vorherige Seite: Gruppen Inhalt Index
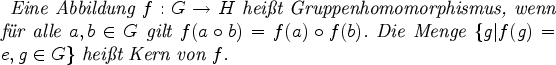
![]()
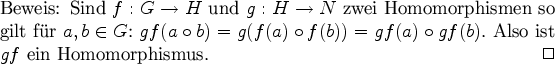

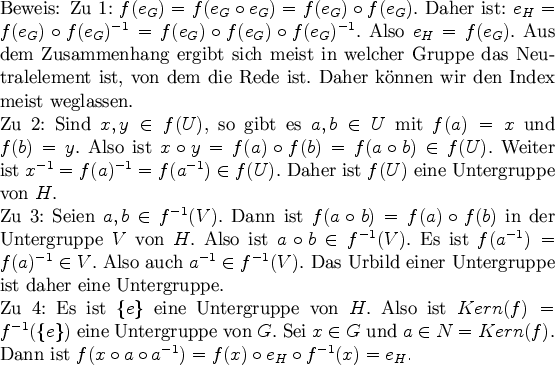
![]()
In einer abelschen Gruppe ist jede Untergruppe auch
Normalteiler. Ist G eine Gruppe, so kann man auf
![]() eine assoziative Verknüpfung erklären. Und zwar:
AoB : = {aob| a
eine assoziative Verknüpfung erklären. Und zwar:
AoB : = {aob| a ![]() A undb
A undb ![]() B}. Für eine Untergruppe
U
B}. Für eine Untergruppe
U ![]() G gilt dann
UoU = U. Ist N ein Normalteiler , so ist für alle
x, y
G gilt dann
UoU = U. Ist N ein Normalteiler , so ist für alle
x, y ![]() G:
xNoyN = (xN)o(Ny) = x(Ny) = xyN.
G:
xNoyN = (xN)o(Ny) = x(Ny) = xyN.
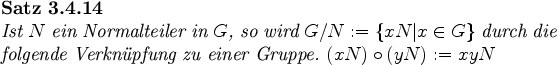

Andreas 2006-12-05