Gruppen

Wollen wir das Reich der Zahlen tiefer kennen lernen, so sollten wir unser begriffliches Werkzeug verfeinern. Ist M eine Menge und g : M×M $\rightarrow$ M eine Abbildung so nennen wir g eine Verknüpfung auf M. Die Verknüpfung g : M×M heißt assoziativ, wenn g(a, g(b, c)) = g(g(a, b), c) ist für alle a, b, c $\in$ M. Dies liest sich etwas ungewohnt. Wählen wir o als Verknüfungszeichen und schreiben es zwischen die Argumente, so zeigt sich das Assoziativgesetz wie gewohnt: ao(boc) = (aob)oc für alle a, b, c $\in$ M. In einer funktionalen Programmiersprache wie Lisp steht der Operator stets vor den Argumenten. Es ist daher nicht überflüssig, sich auch mit der funktionalen Schreibweise bekannt zu machen.

$\begin{definition} Das Paar $(G,\circ)$\ heißt Gruppe, \index{Gruppe}, wenn $G$... ...ex{Gruppe!kommutativ} \index{Gruppe!abelsch} \end{description}\end{definition}$

$\begin{bemerkung} \begin{enumerate} \item In jeder Gruppe gibt es genau ein Ne... ...tem Es ist $(a\circ b)^{-1}=b^{-1}\circ a^{-1}$. \end{enumerate}\end{bemerkung}$

$\begin{Beweis} \begin{enumerate} \item Seien $e_{1}$\ und $e_{2}$\ Neutralelem... ...\circ b^{-1})\circ a^{-1}=a\circ e\circ a^{-1}=e$. \end{enumerate}\end{Beweis}$

Beispiele:

$\mbox{$\mathbb{N}$}$ ist keine Gruppe. Das Inversgesetz ist verletzt.
$\mbox{$\mathbb Z$}$ , $\mbox{$\mathbb Q$}$ , $\mbox{$\mathbb{R}$}$ sind bezüglich der Addition Gruppen.
Für jede ganze Zahl macht die Abbildung

+ : $\displaystyle \mbox{$\mathbb Z /{m} \mathbb Z$}$ × $\displaystyle \mbox{$\mathbb Z /{m} \mathbb Z$}$ $\displaystyle \ni$ (a, b) $\displaystyle \mapsto$ (a + b) modm $\displaystyle \in$ $\displaystyle \mbox{$\mathbb Z /{m} \mathbb Z$}$

aus $\mbox{$\mathbb Z /{m} \mathbb Z$}$ eine Gruppe bezüglich der Addition.
$\mbox{$\mathbb Q$}$ ^* = $\mbox{$\mathbb Q$}$ $\setminus$ {0} ist bezüglich der Multiplikation Gruppen. Genauso ist dies für $\mbox{$\mathbb{R}$}$ ^* der Fall.
Wichtige Gruppen erhält man durch Paarbildung. So bildet die Menge der Zahlenpaare $\mbox{$\mathbb{R}$}$ $\oplus$ $\mbox{$\mathbb{R}$}$ eine Gruppe, wenn man komponentenweise addiert. Das heißt:

(a, b) + (c, d ): = (a + c, b + d )

Das entspricht dann der gewöhnlichen Vektoraddition. Zwei Vektoren spannen ein Parallelogramm auf. Die Diagonale dieses Parallelogramm ist die Summe der beiden Vektoren.

Sind A, B Teilmengen von G, dann ist AoB = {aob| a $\in$ A, b $\in$ B} und A^-1 = {a^-1| a $\in$ A}.
$\begin{definition} Eine nichtleere Teilmenge $U\subset G$\ heißt Untergruppe vo... ...rc U\subset U$\ und $U^{-1}\subset U$\ ist. \index{Untergruppe} \end{definition}$
Der Durchschnitt von Untergruppen ist eine Untergruppe. Jede Teilmenge E $\subset$ G einer Gruppe G ist daher in einer kleinstmöglichen Untergruppe enthalten [E]. Es ist

[E] = $\displaystyle \bigcap$ {U| U Untergruppe vonG undE $\displaystyle \subset$ U}

Diese Untergruppe [E] heißt die von E erzeugte Untergruppe. Beispiele:

Die Untergruppen von $\mbox{$\mathbb Z$}$ sind von der Form m^. $\mbox{$\mathbb Z$}$

Aufgaben:

Ist a $\in$ $\mbox{$\mathbb Q$}$ , so sei [a] = $\mbox{$\mathbb Z$}$ ^.a die kleinste Untergruppe von ( $\mbox{$\mathbb Q$}$ , +), die a enthält.
1. Zeige $\mbox{$\mathbb Z$}$ + $\mbox{$\mathbb Z$}$ ^. ${\frac{{2}}{{3}}}$ ist zyklisch. Welches Element erzeugt $\mbox{$\mathbb Z$}$ + $\mbox{$\mathbb Z$}$ ^. ${\frac{{2}}{{3}}}$ ?
2. Zeige $\mbox{$\mathbb Z$}$ + $\mbox{$\mathbb Z$}$ ^. ${\frac{{2}}{{3}}}$ + $\mbox{$\mathbb Z$}$ ^. ${\frac{{3}}{{5}}}$ ist zyklisch. Welches Element erzeugt die Gruppe?
3. Ist jede von endlich vielen Elementen erzeugte Untergruppe von $\mbox{$\mathbb Q$}$ zyklisch?

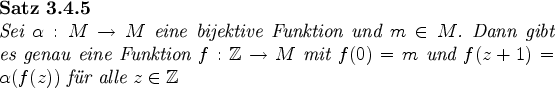
$\begin{satz} Sei $\alpha:M\rightarrow M$\ eine bijektive Funktion und $m\in M$.... ...0)=m$\ und $f(z+1)=\alpha(f(z))$\ für alle $z\in \mbox{$\mathbb Z$}$ \end{satz}$

$\begin{Beweis} Nach dem Rekursionssatz gibt es genau ein $f_{1}:\mbox{$\mathbb{... ...{-1}f_{2}(z+1)= \alpha^{-1}f(z+1)$. Daher ist $\alpha f(z)=f(z+1)$ \end{Beweis}$
Die Untergruppen von $\mbox{$\mathbb Z$}$ kennen wir schon. Es sind genau die Mengen d $\mbox{$\mathbb Z$}$ mit d $\in$ $\mbox{$\mathbb Z$}$ . Nun wollen wir die Untergruppen von $\mbox{$\mathbb Z$}$ × $\mbox{$\mathbb Z$}$ kennzeichnen.

Bild 2.1: Auf einer Geraden

$\includegraphics[width=0.8\textwidth]{/home/andreas/tex/mathematik/Zahlentheorie/buchneu/bilder/bilder.2}$

Schauen wir uns die nebenstehende Zeichnung an, so legt der Strahlensatz die folgende Definition nahe.
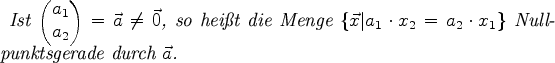
$\begin{definition} Ist $ \begin{pmatrix} a_{1}\\ a_{2} \end{pmatrix}=\vec{... ...$\ Nullpunktsgerade durch $\vec{a}$\index{Nullpunktsgerade}. \end{definition}$
Ich kürze sie mit ng( $\vec{{a}}\,$ ) ab.

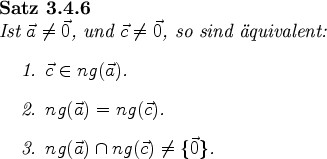
$\begin{satz} Ist $\vec{a}\neq \vec{0}$, und $\vec{c}\neq \vec{0}$, so sind äqui... ... \item $ng(\vec{a})\cap ng(\vec{c})\neq \{\vec{0}\}$. \end{enumerate}\end{satz}$

$\begin{Beweis} \par \noindent 1. \mbox{$\Longrightarrow $}2.: Sei $\vec{c}\in n... ...}d_{1}(c_{1}/d_{1})=a_{2}c_{1}$. Also ist $\vec{c}\in ng(\vec{a})$. \end{Beweis}$

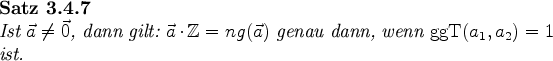
$\begin{satz} Ist $\vec{a}\neq \vec{0}$, dann gilt: $\vec{a}\cdot \mbox{$\mathbb... ...(\vec{a})$\ genau dann, wenn $\mathop{\rm ggT}(a_{1},a_{2})=1$\ ist. \end{satz}$

$\begin{Beweis} Es sei $d=\mathop{\rm ggT}(a_{1},b_{1})=1$. Ist $\vec{c}\in ng(\... ..., u_{2}$\ gleich $0$\ ist, folgt $1=d\cdot z$. Also ist $d=\pm 1$. \end{Beweis}$

Folgerung
Zu jeder Nullpunktsgeraden ng( $\vec{{a}}\,$ ) gibt es teilerfremde u₁, u₂ $\in$ $\mbox{$\mathbb Z$}$ mit ng( $\vec{{a}}\,$ ) = $\left(\vphantom{\begin{array}{c} u_{1}\\ u_{2}\\ \end{array}}\right.$ $\begin{array}{c} u_{1}\\ u_{2}\\ \end{array}$ $\left.\vphantom{\begin{array}{c} u_{1}\\ u_{2}\\ \end{array}}\right)$ $\mbox{$\mathbb Z$}$ = $\vec{{u}}\,$ $\mbox{$\mathbb Z$}$ .

Wir hatten festgestellt, dass zwei Punkte $\vec{{a}}\,$ , $\vec{{b}}\,$ auf einer Geraden durch den Nullpunkt liegen, wenn a₁^.b₂ = a₂^.b₁ das heßt a₁^.b₂ - a₂^.b₁ = 0 ist. Dieser Term, er hängt von $\vec{{a}}\,$ und $\vec{{b}}\,$ ab, hat eine anschauliche Bedeutung. Er gibt dem Betrage nach den Flächeninhalt des von $\vec{{a}}\,$ und $\vec{{b}}\,$ aufgespannten Parallelogramms an.
$\begin{definition} $\det(\vec{a},\vec{b})= \begin{vmatrix} a_{1}&b_{1}\\ a_... ...Determinante von $\vec{a}$\ und $\vec{b}$.\index{Determinante} \end{definition}$

**Bild 2.2:** Determinante
$\includegraphics[width=0.8\textwidth]{/home/andreas/tex/mathematik/Zahlentheorie/buchneu/bilder/bilder.3}$

Betrachtet man die Zeichnung nebenan, so leuchtet die geometrische Bedeutung der Determinante ein. Die Fläche des Parallelogramms ist:

(a₁ + b₁)^.(a₂ + b₂) - 2b₁a₂ - a₁^.a₂ - b₁^.b₂ = a₁b₂ - a₂b₁.

Die Determinante gibt daher den orientierten Flächeninhalt des von $\vec{{a}}\,$ und $\vec{{b}}\,$ aufgespannten Parallelogramms an.

Algebraisch hat sie folgende Eigenschaften:

$\begin{satz}[Determinante] \begin{enumerate} \item Für alle $\vec{a},\vec{b},\... ...ec{a},\vec{b}\times z)=\det(\vec{a},\vec{b})\cdot z$. \end{enumerate}\end{satz}$

$\begin{Beweis} Dies ist alles leicht nachzurechen. \end{Beweis}$
Jede dieser zunächst rein formalen Eigenschaften bedeutet geometrisch etwas. Mache Dir das klar.

Folgerung
Ist U eine Untergruppe von $\mbox{$\mathbb Z$}$ × $\mbox{$\mathbb Z$}$ , so gilt:

Für alle $\vec{{a}}\,$ $\in$ $\mbox{$\mathbb Z$}$ × $\mbox{$\mathbb Z$}$ ist die Menge d ( $\vec{{a}}\,$ , U) : = {det( $\vec{{a}}\,$ , $\vec{{u}}\,$ )| $\vec{{u}}\,$ $\in$ U} eine Untergruppe von $\mbox{$\mathbb Z$}$ . Es gibt daher ein n $\in$ $\mbox{$\mathbb Z$}$ mit d ( $\vec{{a}}\,$ , U) = n^. $\mbox{$\mathbb Z$}$ .
Die Menge d (U, U) = {det( $\vec{{u}}\,$ , $\vec{{v}}\,$ )| $\vec{{u}}\,$ , $\vec{{v}}\,$ $\in$ U} ist eine Untergruppe von $\mbox{$\mathbb Z$}$ .

$\begin{Beweis} Dies ist zum Nachrechnen. \end{Beweis}$

$\begin{satz} Jede Untergruppe von $U$\ ist von höchstens zwei Elementen erzeugt. \end{satz}$

$\begin{Beweis} Ist $U=\{\vec{0}\}$, so ist nichts zu zeigen. Ist $U\neq \{\vec{... ... x\cdot y$\ für ein $x\in \mbox{$\mathbb Z$}$. Es folgt: $y=\pm 1$. \end{Beweis}$

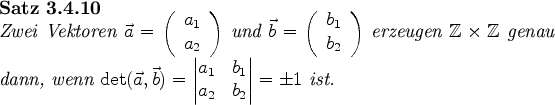
$\begin{satz} Zwei Vektoren $\vec{a}=\left(\begin{array}{c} a_{1}\\ a_{2}\\ ... ...)=\begin{vmatrix}a_{1}&b_{1}\\ a_{2}&b_{2}\end{vmatrix}=\pm 1$\ ist. \end{satz}$

$\begin{Beweis} Es gibt $x,y\in \mbox{$\mathbb Z$}$\ mit $\vec{a}x+\vec{b}y=\lef... ...}y'=1$. Daher sind $a_{2},b_{2}$\ teilerfremd. Also ist $d=\pm 1$. \end{Beweis}$

Folgerung
ng( $\vec{{a}}\,$ ) ist die größte zyklische Untergruppe von $\mbox{$\mathbb Z$}$ × $\mbox{$\mathbb Z$}$ , welche $\vec{{a}}\,$ enthält.

Wir betrachten in den folgenden Aufgaben Gleichungen vom Typ:

a^.x + b^.y = c

(3.1)

mit a, b, c $\in$ $\mbox{$\mathbb Z$}$ . Man nennt diese Gleichung eine lineare diophantische Gleichung. Ein Vektor $\left(\vphantom{\begin{array}{c} x'\\ y'\\ \end{array}}\right.$ $\begin{array}{c} x'\\ y'\\ \end{array}$ $\left.\vphantom{\begin{array}{c} x'\\ y'\\ \end{array}}\right)$ $\in$ $\mbox{$\mathbb Z$}$ × $\mbox{$\mathbb Z$}$ heißt Lösung der Gleichung, wenn a^.x' + b^.y' = c ist. So ist $\left(\vphantom{\begin{array}{c} 2\\ -1\\ \end{array}}\right.$ $\begin{array}{c} 2\\ -1\\ \end{array}$ $\left.\vphantom{\begin{array}{c} 2\\ -1\\ \end{array}}\right)$ Lösung der Gleichung 2x + 3y = 1.

Aufgaben:

Es sei eine Gleichung der Form gegeben.
1. Betrachte die Gleichung 2x + 4y = 0, x, y $\in$ $\mbox{$\mathbb Z$}$ . Zeige: Die Lösungsmenge ist eine Gittergerade durch den Nullpunkt. Berechne die Gerade.
2. Gegeben ist die Gittergerade durch den Nullpunkt: g = $\left(\vphantom{\begin{array}{c} 5\\ 3\\ \end{array}}\right.$ $\begin{array}{c} 5\\ 3\\ \end{array}$ $\left.\vphantom{\begin{array}{c} 5\\ 3\\ \end{array}}\right)$ $\mbox{$\mathbb Z$}$ . Gibt es eine Gleichung der Form derart, dass g Lösungsmenge der Gleichung ist. Wenn ja berechne diese Gleichung.
3. Gibt es zu g = $\left(\vphantom{\begin{array}{c} 6\\ 9\\ \end{array}}\right.$ $\begin{array}{c} 6\\ 9\\ \end{array}$ $\left.\vphantom{\begin{array}{c} 6\\ 9\\ \end{array}}\right)$ $\mbox{$\mathbb Z$}$ eine Gleichung der Art ?
4. Gib eine notwendige und hinreichende Bedingung für c, d $\in$ $\mbox{$\mathbb Z$}$ an, so dass g = $\left(\vphantom{\begin{array}{c} c\\ d\\ \end{array}}\right.$ $\begin{array}{c} c\\ d\\ \end{array}$ $\left.\vphantom{\begin{array}{c} c\\ d\\ \end{array}}\right)$ $\mbox{$\mathbb Z$}$ Lösungsmenge einer Gleichung der Form ist.
5. Zeige: Die Menge der Zahlen, deren Summe durch 3 teilbar ist bildet eine Untergruppe U von $\mbox{$\mathbb Z$}$ × $\mbox{$\mathbb Z$}$ . Bestimme $\vec{{a}}\,$ , $\vec{{b}}\,$ $\in$ $\mbox{$\mathbb Z$}$ derart, dass $\vec{{a}}\,$ $\mbox{$\mathbb Z$}$ + $\vec{{b}}\,$ $\mbox{$\mathbb Z$}$ = U ist.

$\begin{definition} Für eine Untergruppe $U$\ und ein $a\in G$\ ist $aU=\{au\ver... ...nebenklasse. \index{Linksnebenklasse}\index{Rechtsnebenklasse} \end{definition}$
Beispiele:

Ist u $\in$ U, so ist u^.U = U^.u = U.
Sei m $\in$ $\mbox{$\mathbb{N}$}$ . U = m $\mbox{$\mathbb Z$}$ ist Untergruppe von $\mbox{$\mathbb Z$}$ . Die Nebenklassen von U sin die mengen der Form k + m $\mbox{$\mathbb Z$}$ mit k $\in$ {0,..., m - 1}.
Die Gruppenoperation ist die Addition. Eine Nebenklasse N von U schreibt sich: N = z + m $\mbox{$\mathbb Z$}$ mit z $\in$ $\mbox{$\mathbb Z$}$ . Es ist z + U = (- z) + U. Daher kann z $\in$ $\mbox{$\mathbb{N}$}$ angenommen werden. Es ist z = q^.m + r mit q $\in$ $\mbox{$\mathbb{N}$}$ und r $\in$ {0,..., m - 1}. Es folgt N = z + U = r + q^.m + m $\mbox{$\mathbb Z$}$ = r + m $\mbox{$\mathbb Z$}$ . Daher ist N von der gewünschten Form.
Ist U $\subset$ $\mbox{$\mathbb Z$}$ × $\mbox{$\mathbb Z$}$ eine zyklische Untergruppe, so sind die Nebenklassen gerade die zu U parallelen Geraden.

$\begin{bemerkung} Ist $U$\ eine endliche Untergruppe von $G$, so haben alle Rec... ... alle Linksnebenklassen von $U$\ genau soviel Elemente wie $U$. \end{bemerkung}$

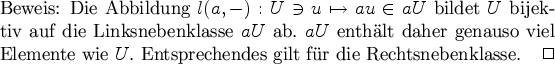
$\begin{Beweis} Die Abbildung $l(a,-):U\ni u \mapsto au\in aU$\ bildet $U$\ bije... ...l Elemente wie $U$. Entsprechendes gilt für die Rechtsnebenklasse. \end{Beweis}$

$\begin{bemerkung} Zwei Nebenklassen sind entweder gleich oder haben keine Elemente gemeinsam. \end{bemerkung}$

$\begin{Beweis} Angenommen die beiden Nebenklassen $aU$\ und $bU$\ haben ein gem... ...\subset aU$. Genauso ist $aU\subset bU$. Das heißt es ist $aU=bU$. \end{Beweis}$

$\begin{bemerkung} Jede Gruppe ist elementfremde Vereinigung seiner Rechtsnebenk... ...sweise seiner Linksnebenklassen bezüglich einer Untergruppe $U$. \end{bemerkung}$
Dies ist jetzt klar.
$\begin{definition} Ist die Gruppe $G$\ endlich, so heißt die Anzahl ihrer Eleme... ...x von $U$\ in $G$\ abgekürzt $[U:G]$.\index{Index!Untergruppe} \end{definition}$

$\begin{satz} Es ist $ord(G)=[U:G]\cdot ord(U)$. \end{satz}$

$\begin{Beweis} Es ist $G$\ die elementfremde Vereinigung aller Rechtsnebenklass... ...]$\ verschiedene solcher Nebenklassen. Daher folgt die Behauptung. \end{Beweis}$

Folgerung
Jede Gruppe, deren Ordnung eine Primzahl ist, wird von einem Element erzeugt.

$\begin{Beweis} Da $ord(G)=p$\ eine Primzahl ist, gibt es mindestens ein $e\neq ... ... von $G$. Also ist $ord(x)=ord(G)$. Daher erzeugt $x$\ die Gruppe. \end{Beweis}$

Andreas 2006-12-05