-
2n > 10000 für fast alle
n

 .
.
- 2n > n2 für fast alle
n

 .
.
- 2n > n3 für fast alle
n

 .
.
- Ist a > 1, und c beliebig aus
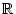 , dann ist an > c.
für fast alle
n
, dann ist an > c.
für fast alle
n 
 .
.
Also für fast alle
n 
 ist
ist
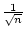

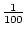 . Dies ist aber nicht nur
für
. Dies ist aber nicht nur
für
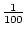 richtig.
Sei dazu
richtig.
Sei dazu
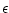 > 0 gegeben.
Dann hat man folgende Äquivalenz:
> 0 gegeben.
Dann hat man folgende Äquivalenz:
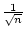

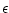
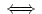
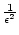
 n.
Dies ist nach dem Axiom von Archimedes für ein
k
n.
Dies ist nach dem Axiom von Archimedes für ein
k 
 richtig
und infolgedessen erst recht für alle n > k.
Das heißt für fast alle
n
richtig
und infolgedessen erst recht für alle n > k.
Das heißt für fast alle
n 
 ist
ist
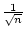

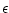 .
Dabei war das
.
Dabei war das
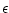 > 0 völlig beliebig gewählt.
Wir erklären:
> 0 völlig beliebig gewählt.
Wir erklären:
Definition 1.2.8
Eine Folge heißt Nullfolge genau dann, wenn für jedes
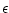 > 0
gilt: Für fast alle
n
> 0
gilt: Für fast alle
n 
 : | an| <
: | an| < 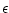 .
Bezeichnung:
.
Bezeichnung:
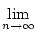 (an) = 0.
(an) = 0.
Satz 1.2.2
Folgende Aussagen sind äquivalent:
-
 ist unbeschränkt. (Axiom von Archimedes)
ist unbeschränkt. (Axiom von Archimedes)
-
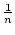 ist eine Nullfolge.
ist eine Nullfolge.
Beweis:1.
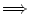 2.:
Sei
2.:
Sei
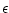 > 0 gegeben. Dann gibt es ein
k
> 0 gegeben. Dann gibt es ein
k 
 mit:
mit:
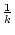 <
< 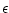 . Für alle n
. Für alle n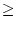 k gilt dann erst recht
k gilt dann erst recht
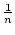

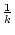 <
< 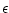 . Also ist für fast alle
n
. Also ist für fast alle
n 
 :
: 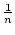 <
< 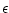 .
.
2.
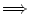 1.:
Sei c > 0. Wir zeigen, dass c keine obere Schranke
von
1.:
Sei c > 0. Wir zeigen, dass c keine obere Schranke
von
 sein kann. Da
sein kann. Da
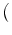
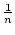
 eine Nullfolge ist, ist
für fast alle
n
eine Nullfolge ist, ist
für fast alle
n 
 :
: 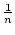 <
< 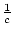 .
Also ist für fast
alle
n
.
Also ist für fast
alle
n 
 : c < n. Daher kann natürlich c keine
obere Schranke von
: c < n. Daher kann natürlich c keine
obere Schranke von
 sein.
sein. 
Satz 1.2.3
Jede Nullfolge ist beschränkt.
Beweis:Sei (an) eine Nullfolge. Dann ist | an| < 1 für fast
alle
n 
 . Sind schon alle | an| < 1, dann ist schon -1 eine
untere Schranke von (an) und es gilt:
-1 < an < 1 für alle
n
. Sind schon alle | an| < 1, dann ist schon -1 eine
untere Schranke von (an) und es gilt:
-1 < an < 1 für alle
n 
 .
Andernfalls gibt es nur endlich viele an mit:
1 < | an|. Unter diesen endlich vielen an gibt es ein
größtes | ak| = C. Dann ist für alle
n
.
Andernfalls gibt es nur endlich viele an mit:
1 < | an|. Unter diesen endlich vielen an gibt es ein
größtes | ak| = C. Dann ist für alle
n 
 : - C < | an| < C. Damit ist die Behauptung gezeigt.
: - C < | an| < C. Damit ist die Behauptung gezeigt. 
Satz 1.2.4
- Sind (an) und (bn) Nullfolgen, dann ist (an + bn)
eine Nullfolge.
- Ist
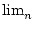 (an) = 0 und (bn) beschränkt, dann ist
(anbn) eine Nullfolge.
(an) = 0 und (bn) beschränkt, dann ist
(anbn) eine Nullfolge.
- Ist
lim(bn) = 0 und
| an|
 | bn| für fast alle
n
| bn| für fast alle
n 
 ,
dann ist
,
dann ist
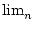 (an) = 0. Man sagt die Folge
(bn) ist eine Majorante der Folge (an).
(an) = 0. Man sagt die Folge
(bn) ist eine Majorante der Folge (an).
Beweis:Zu 1.: Sei 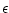 eine winzig kleine Zahl > 0. Dann ist für
fast alle
n
eine winzig kleine Zahl > 0. Dann ist für
fast alle
n 
 :
:
1)
| an| < 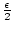 und
und
2)
| bn| < 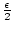 und also :
und also :
| an + bn| | an| + | bn| <
| an| + | bn| < 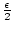 +
+ 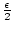 =
= 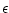 für fast alle
n
für fast alle
n 
 .
.
Zu 2.: C eine obere Schranke von (| bn|). Sei nun
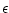 > 0.
Dann ist für fast alle
n
> 0.
Dann ist für fast alle
n 
 : | an| <
: | an| < 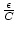 . Damit
| anbn| = | an|| bn|
. Damit
| anbn| = | an|| bn|
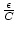 . | bn|
. | bn|
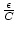 . C =
. C = 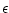 für
fast alle
n
für
fast alle
n 
 . Daraus ergibt sich die
Behauptung.
. Daraus ergibt sich die
Behauptung.
Zu 3.:Einfachst. 
Sprechweise:
Ist (an) eine Nullfolge, deren Folgenglieder fast
alle 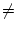 0 sind, so sagt man (an) ist eine ,,unendlich kleine Zahl``.
Achtung!!!. (an) ist dann keine Zahl, sondern eine Folge.
Sie wird gegen das ,,Ende`` hin kleiner als jede vorher gewählte positive
Zahl.
Schreibweise:
dx = (an). Ist
dx = (an) eine unendlich kleine Zahl
und an > 0 für fast alle
n
0 sind, so sagt man (an) ist eine ,,unendlich kleine Zahl``.
Achtung!!!. (an) ist dann keine Zahl, sondern eine Folge.
Sie wird gegen das ,,Ende`` hin kleiner als jede vorher gewählte positive
Zahl.
Schreibweise:
dx = (an). Ist
dx = (an) eine unendlich kleine Zahl
und an > 0 für fast alle
n 
 ,
so nennt man dx größer 0. dx > 0.
Entsprechend für dx < 0.
Mit dieser Bezeichnung kann man obigen Satz
vieleicht etwas eingängiger formulieren.
,
so nennt man dx größer 0. dx > 0.
Entsprechend für dx < 0.
Mit dieser Bezeichnung kann man obigen Satz
vieleicht etwas eingängiger formulieren.
- Die Summe unendlich kleiner Zahlen ist unendlich
klein.
- Das Produkt aus etwas beschränktem und einer
unendlich kleinen Zahl, ist unendlich klein.
- Ist dx unendlich klein und
0 < dy < dx , dann
ist dy unendlich klein.
Andreas Bartholome
2003-11-26
![]() 1.:
Sei c > 0. Wir zeigen, dass c keine obere Schranke
von
1.:
Sei c > 0. Wir zeigen, dass c keine obere Schranke
von
![]() sein kann. Da
sein kann. Da
![]()
![]()
![]() eine Nullfolge ist, ist
für fast alle
n
eine Nullfolge ist, ist
für fast alle
n ![]()
![]() :
: ![]() <
< ![]() .
Also ist für fast
alle
n
.
Also ist für fast
alle
n ![]()
![]() : c < n. Daher kann natürlich c keine
obere Schranke von
: c < n. Daher kann natürlich c keine
obere Schranke von
![]() sein.
sein. ![]()
![]() und
und
![]() und also :
und also :
![]() | an| + | bn| <
| an| + | bn| < ![]() +
+ ![]() =
= ![]() für fast alle
n
für fast alle
n ![]()
![]() .
.
![]() > 0.
Dann ist für fast alle
n
> 0.
Dann ist für fast alle
n ![]()
![]() : | an| <
: | an| < ![]() . Damit
| anbn| = | an|| bn|
. Damit
| anbn| = | an|| bn|![]()
![]() . | bn|
. | bn|![]()
![]() . C =
. C = ![]() für
fast alle
n
für
fast alle
n ![]()
![]() . Daraus ergibt sich die
Behauptung.
. Daraus ergibt sich die
Behauptung.
![]()
![]() 0 sind, so sagt man (an) ist eine ,,unendlich kleine Zahl``.
Achtung!!!. (an) ist dann keine Zahl, sondern eine Folge.
Sie wird gegen das ,,Ende`` hin kleiner als jede vorher gewählte positive
Zahl.
Schreibweise:
dx = (an). Ist
dx = (an) eine unendlich kleine Zahl
und an > 0 für fast alle
n
0 sind, so sagt man (an) ist eine ,,unendlich kleine Zahl``.
Achtung!!!. (an) ist dann keine Zahl, sondern eine Folge.
Sie wird gegen das ,,Ende`` hin kleiner als jede vorher gewählte positive
Zahl.
Schreibweise:
dx = (an). Ist
dx = (an) eine unendlich kleine Zahl
und an > 0 für fast alle
n ![]()
![]() ,
so nennt man dx größer 0. dx > 0.
Entsprechend für dx < 0.
Mit dieser Bezeichnung kann man obigen Satz
vieleicht etwas eingängiger formulieren.
,
so nennt man dx größer 0. dx > 0.
Entsprechend für dx < 0.
Mit dieser Bezeichnung kann man obigen Satz
vieleicht etwas eingängiger formulieren.