Kreis-Primzahlen

Eine bisher offene Frage ist: Ist p eine Primzahl, so heißt 2^p - 1 eine Mersenne-Zahl. Ist 2^p - 1 eine Primzahl, so heißt sie Mersenne Primzahl. Eine offene Frage ist:

Fr.1:

Gibt es unendlich viele Mersenne Primzahlen? Über diese Frage denken viele Leute intensiv nach. Es gibt eine Jagt nach der größten Mersenne Primzahl. Das ist eine Herausforderung an Computer, Programmierer und Mathematiker. Man kann diese Frage folgendermaßen interpretieren:

2^p -1 = 1 + 2 + 2² + ... +2^p-1 = $\Phi_{{p}}^{}$(2). Dabei ist $\Phi_{{p}}^{}$(X) das pte Kreisteilungspolynom. Die Frage lautet also: Für welche Primzahlen ist $\Phi_{{p}}^{}$(2) eine Primzahl? Macht man sich unabhängig von der Basis 2, so erhält man die Frage:

Fr.2:

Gegeben ist eine natürliche Zahl a$\ge$2. Für welche Primzahlen p ist $\Phi_{{p}}^{}$(a) eine Primzahl? Das lässt sich auch anders ausdrücken. Welche Repunits zur Basis a sind Primzahlen? Eine Repunit ist eine Zahl, unter deren Ziffern nur die 1 vorkommt. Beispielsweise 11 im 10er System.

Fr.3:

Fermat vermutete: Alle Zahlen der Form F_n = 2²ⁿ + 1 sind Primzahlen. Er wurde von Euler widerlegt. Seitdem gehört es zum beliebten Sport Fermat-Zahlen zu zerlegen. Hiefü+r ist sehr viel Mathematik notwendig. Denn Faktorisieren ist ein schwieriges Geschäft. Die sehr große Fermat-Zahl F₉ wurde 1990 zerlegt. Viel früher (1953) kannte man schon Faktoren der Zahl F₁₀. Deuten wir die Frage um:

-

$\Phi_{{2}}^{}$(2) = 2 + 1 = 3

 $&bull#bullet;$

$\Phi_{{4}}^{}$(2) = $\Phi_{{2}}^{}$(2²) = 5.

 $&bull#bullet;$

$\Phi_{{2^{3}}}^{}$(2) = $\Phi_{{2}}^{}$(2⁴) = 17

Also welche Zahlen der Form $\Phi_{{2^{n}}}^{}$(2) sind Primzahlen? Auch hier kann man sich von der basis befreien. Natürlich muss die Basis gerade sein. Die Frage ist daher: Welche Zahlen der Form $\Phi_{{2^{n}}}^{}$(a) sind Primzahlen bei gegebenem a.

Beispielsweise:

-

$\Phi_{{2}}^{}$(6) = 6 + 1 = 7 ist prim.

-

$\Phi_{{2^{2}}}^{}$(6) = 37 ist prim. ...

Fr.4:

Wann ist $\Phi_{{3^{n}}}^{}$(2) Primzahl?

-

$\Phi_{{3}}^{}$(2) = 7 ist prim.

-

$\Phi_{{9}}^{}$(2) = $\Phi_{{3}}^{}$(2³) = 2⁶ +2³ + 1 = 73 ist prim.

-

$\Phi_{{81}}^{}$(2) = 2⁵⁴ +2²⁷ + 1 = 18014398643699713. Diese Zahl ist nicht prim. Die Faktorisierung ist: 18014398643699713 = 2593 ^. 71119 ^. 97685839.

-

Auch $\Phi_{{243}}^{}$(2) ist nicht prim. Ein Faktor ist 487. Dies ist leicht bestätigten. Der Quotient ist leider noch sehr groß nämlich:

12004120224483802202905013857734643342673674711.

Is er prim? Zur Basis 2 ist diese Zahl p pseudoprim. Denn es ist 2^p = 2 mod p. Zur Basis 3 ergibt sich aber

3^p = 11194885745470593499729871386133934452446851430 mod p.

Also kann die Zahl nicht prim sein. Ich kann sie aber mit meinen Mitteln nicht zerlegen.

Fr.5:

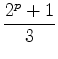Für welche Primzahlen ist $${\frac{{2^{p}+1}}{{3}}}$$ wieder eine Primzal? Das sind Primzahlen der Form: $\phi_{{2\cdot p}}^{}$(2). Dabei ist p eine ungerade Primzahl.

Eine erste Tabelle liefert:

p	Wert	Eigenschaft
3	3	prim
5	11	prim
7	43	prim
11	683	prim
13	2731	prim
17	43691	prim
19	174763	prim
23	2796203	prim
29	178956971	nicht prim
31	715827883	prim
37	45812984491	nicht prim
39	183251937963	nicht prim
41	733007751851	nicht prim
43	2932031007403	prim
47	46912496118443	nicht prim
53	3002399751580331	nicht prim
59	192153584101141163	nicht prim
61	768614336404564651	prim.
67	49191317529892137643	nicht prim

Kandidaten für Primzahlen von dieser Form sind: p = 73, 79, 101, 127 die anderen bestehen den Pseudoprimzahltest nicht.