Lösungen

Lösungen:

1. 1. $f(n)=n³+11n=n³+5n\bmod 6$. Die Wertetabelle dieser Funktion sieht so aus:

      0	1	2	3	4	5
      0	0	0	0	0	0

      Daher ist n³ +11 ^. n für alle n $\in$ $\mbox{$\mathbb{N}$}$ durch 6 teilbar.
   2. Wegen Satz 2.4.3 muss nur untersucht werden ob 6 und 7 Teiler von f (n) = n⁷ - n durch 7 und 6 teilbar sind. Die Wertetabelle modulo 7 ist

      0	1	2	3	4	5	6
      0	0	0	0	0	0	0

      Auch bei der Wertetabelle modulo 6 bestätigt man leicht, dass sich stets der Wert 0 ergibt.
   3. Es ist 12⁴ = 1 mod 4147. Daher ist 12⁵¹² - 1 durch 4147 teilbar.
   4. Es ist 104975 = 5^{2 .} 13 ^. 17 ^. 19. Wir brauchen also wegen Satz 2.4.3 nur zu testen ob die Zahl durch 13, 17, 19, 25 teilbar ist.

      
      

      $$\equiv \left(\vphantom{5^{4}}\right. \left.\vphantom{5^{4}}\right)^{{32}}_{}$$ = 0 mod 13

      $$\equiv$$ = 0 mod 17

      $$\left(\vphantom{18^{2}}\right. \left.\vphantom{18^{2}}\right)^{{64}}_{}$$ = 0 mod 19

      $$\left(\vphantom{18^{4}}\right. \left.\vphantom{18^{4}}\right)^{{32}}_{}$$ = 0 mod 25

      
      Also ist 18¹²⁸ - 1 durch 104975 teilbar.
   5. Schreibt man die verschiedenen Potenzen von 2, die ,,Bahn`` von 2 modulo 13 auf, so erhält man: 1, 2, 4, 8, 3, 6, 12, 11, 9, 5, 10, 7, 1. Das heißt 2¹² = 1 mod 13 und 2¹⁰ = 10 mod 13. Also ist 2⁷⁰ = 10 mod 13. Die Bahn von 3 ist: 1, 3, 9, 1. Das heißt 3⁷⁰ = 3 mod 13. Es ergibt sich: 2⁷⁰ +3⁷⁰ = 10 + 3 = 0 mod 13.
   6. Es ist 48 = 3 ^. 16. Modulo 3 gilt die Kongruenz: 5²ⁿ +24n - 1 $\equiv$ (2²) - 1 = 0 mod 3. Also ist der Term für alle n $\in$ $\mbox{$\mathbb{N}$}$ durch 3 teilbar. Bleibt noch zu überlegen wie es für 16 aussieht. 5²ⁿ +24n - 1 $\equiv$ 9ⁿ +8n - 1 mod 16. Für gerade Zahlen n ist 8 ^. n = 0 mod 16 und 9² = 1 mod 16. Also ist 9ⁿ +8n - 1 = 0 mod 16. Für ungerade Zahlen ist 9ⁿ = 9 mod 16 und 8n = 8 mod 16. Also ist 9ⁿ +8n - 1 = 0 mod 16. Daher ist der Term für alle n $\in$ $\mbox{$\mathbb{N}$}$ durch 16 teilbar.

Zusatzaufgaben

1. Für welche natürlichen Zahlen n $\in$ $\mbox{$\mathbb{N}$}$ ist 2ⁿ +3ⁿ durch 13 teilbar?

Lösungen:

1. 1. Es gibt keine Zahlen n, so dass 4 ^. n² + 1 durch drei teilbar ist. Denn 4 ^. n² +1 $\equiv$ 0 mod 3, bedeutet: n² = 2 mod 3. Dies ist unmöglich.
   2. 4n² +3 = 0 mod 7$\iff$n = ±1 mod 7.
   3. Wir untersuchen zunächst für welche natürlichen Zahlen 2ⁿ -1 = 0 mod 19 gilt.Probiert man ein wenig, so ergibt sich: Die kleinste Zahl m > 0 mit 2^m = 0 mod 19 ist 18. Beh.: 2ⁿ -1 = 0 mod 19 genau dann, wenn n durch 18 teilbar ist. Die eine Richtung der Behauptung ist klar. Denn ist n = k ^. 18 für ein k $\in$ $\mbox{$\mathbb{N}$}$, so ist (2¹⁸)k = 1 mod 19. Ist n eine weitere solche Zahl, so können wir sie durch 18 teilen und erhalten: n = 1 ^. 18 + r mit r < 18. Es folgt: 1 = 2ⁿ = 2^{k . 18+r} = 2^r mod 19. Also ist r = 0.

      Es ist 2⁴ = 16 = - 3 mod 19. Daher ist 2²ⁿ +3 = 2⁴(2^2n-4 -1) = 0 mod 19 genau dann , wenn 2^2n-4 -1 = 0 mod 19 ist. Wir müssen daher untersuchen, für welche n die Zahl 2ⁿ - 4 durch 18 teilbar ist. Dies ist genau dann der Fall, wenn 2^n-2 = 1 mod 9 ist. Genauso wie oben stellt man fest, dass dies genau für die Zahlen n = 2 mod 6 ist. Also hat man als Gesamtergebnis:

      2²ⁿ + 3 ist genau dann durch 19 teilbar, wenn n = 2 mod 6 ist. Beispiele: 2²² +3 = 19 = 0 mod 19, 2²⁸ +3 = 0 mod 19.

   4. Es ist F_n = 2²ⁿ + 1 und daher 2²ⁿ = - 1 modF_n. Daher ist $\left(\vphantom{\displaystyle 2^{2^{n}}}\right.$2²ⁿ$\left.\vphantom{\displaystyle 2^{2^{n}}}\right)^{{2}}_{}$ = 2²ⁿ⁺¹ = 1 modF_n. Weiter ist F_n -1 = 2²ⁿ ein Vielfaches von 2ⁿ⁺¹, da 2ⁿ$\ge$n + 1. Also ist 2²²ⁿ = 1 modF_n. Daher ist 2 ^. 2²²ⁿ -2 = 0 modF_n. Das heißt: 2²²ⁿ⁺¹ -2 = 0 modF_n. Das hin wiederum bedeutet 2^F_n - 2 ist durch F_n teilbar.

2. Fehlt.
3. 1. Wir haben: 1 = 1 mod 7, 11 $\equiv$ 3 + 1 = 4 mod 7, ^... , 111111 $\equiv$ 0 mod 7.

      Beh.: Eine Repunit ist genau dann durch 7 teilbar, wenn die Anzahl der 1er ein Vielfaches von 6 ist.

      Beweis: Sei a eine Repunit, derart, dass die AQnzahl der 1er ein Vielfaches von 6 ist. Dann lässt sich schreiben a = 111111 ^. (1 + 10⁶ + ^... +10^6k). Der erste Faktor ist durch 7 teilbar Also ist auch das Produkt durch 7 teilbar.

      Sei umgekehrt a eine Repunit, die durch 7 teilbar ist. Sei etwas m die Anzahl der 1er von a. Es ist m = 6k + r mit r < 6. Es lässt sich a schreiben a = b ^. 10^r + c, wobei c eine Zahl mit r 1ern ist. b hat 6 ^. k 1er. b ist also durch 7 teilbar. Also muss c durch 7 teilbar sein. Das heißt r = 0. Also ist m ein Vielfaches von 6.

   2. Die Zahl ist selber durch 7 teilbar, denn 1992 mod 7 = 0
   3. Es ist abcdef = 10⁵a + 10⁴b + 10³c + 10²d + 10e + f $\equiv$ 5a + 4b + 6c + 2d + 3e + f mod 7.
   4. Analog.
   5. --

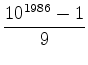4. 1. Die Zahl, die in Rede steht lässt sich schreiben: 1984 ^. (1 + 10⁴ + ^... + (10⁴)¹⁹⁸⁵) = 1984 ^. $${\frac{{10^{1986}-1}}{{9}}}$$. Es ist 10⁶ = 1 mod 7 und 10⁶ = 1 mod 13. Also ist 10¹⁹⁸⁶ - 1 durch 13 ^. 7 teilbar. Außerdem ist 10ⁿ = 1 mod 3. Daher ist die obige Summe durch 3 teilbar. 1984 ist durch 2⁶ teilbar. Insgesamt ergibt sich, dass die betrachtete Zahl durch 2^{6 .} 3 ^. 7 ^. 13 = 17472 teilbar ist.
   2. Für belibiges n ist 10⁶ⁿ - 1 durch 7 teilbar. Das ergibt XXXXXXX ist für beiebiges X durch 7 teilbar.

5. 1. f (x) = x² + x + 1. Ist x $\equiv$ 1 mod 3, so ist f (x) durch 3 teilbar. In allen anderen Fällen nicht.
   2. Es muss x $\equiv$ 1 mod 3 sein. Daher hat man folgende Möglichkeiten:
      1. x $\equiv$ 1 mod 9. Dann ist f (x) = 3 mod 9. Dies ist nicht durch 9 teilbar.
      2. x $\equiv$ 4 mod 9. Dann ist f (x) $\equiv$ 7 + 4 + 1 $\equiv$ 3 mod 9.
      3. x $\equiv$ 7 mod 9. Dann ist f (x) = 4 + 7 + 1 $\equiv$ 3 mod 9.

6. Genauso.
7. 1. f (x) ^. (x - 1) = x⁵ - 1. Die Wertetabelle von x⁵ -1 mod 5 ist:

      0	1	2	3	4
      4	0	1	2	3

      Also nur für x $\equiv$ 1 mod 5 ist x⁵ - 1 durch 5 teilbar. Tatsächlich ist dann auch f (x) durch 5 teilbar.
   2. Angenommen f (x) ist durch 25 teilbar. Dann ist f (x) durch 5 teilbar, wegen Teil a der Aufgabe x = 1 + k ^. 5 für ein k $\in$ $\mbox{$\mathbb Z$}$. Rechnen wir f (x) mod 25 so erhalten wir: f (x) = (1 + k ^. 5)⁰ + (1 + k ^. 5)¹ + (1 + k ^. 5)² + (1 + k ^. 5)³ + (1 + k ^. 5)⁴ = 1 + (1 + k ^. 5) + (1 + 2k ^. 5) + (1 + 3k ^. 5) + (1 + 4k ^. 5) mod 25 = 5 + 5k ^. (1 + 2 + 3 + 4) = 5 mod 25.
   3. --
   4. --