Thalessatz
Thales von Milet wurde ungefähr 625 vor Christus in Milet Kleinasien
geboren und starb ungefähr 547. Er war Naturphilosoph, Mathematiker, Ingenier und Politiker. Als
Kaufmann sagte er in Ägybten richtig die Sonnenfinsternis von 585
v. Christus voraus und erwarb sich dadurch großes Ansehen. Er war einer der
ersten Menschen, die natürliche Ursachen für gewaltige Naturereignisse
suchten. So versuchte er die Erdbeben nicht durch den Zorn der Götter zu
deuten, sondern nach seiner Theorie schwamm die Erde auf einem riesiegen
Wasermeer. Die Wellenbewegungen deises Meeres verursachten die Beben. Von
ihm stammt eine erste Version des folgenden wunderschönen Satzes.
Satz 3.3.1 (Satz des Thales)
- Ist [AB] ein Kreisdurchmesser und C ein Punkt auf dem Halbkreis
über [AB], so ist das Dreieck rechtwinklig bei C.
- Ist das Dreieck rechtwinklig bei C, so liegt C auf dem Kreis
über AB
Beweis:
Abbildung 3.5:
Thalessatz
 |
Sei M der Mittelpunkt von [AB] Dann gilt
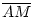 =
= 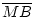 =
= 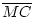 Daher ist
Daher ist
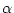 =
= 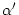 und
und
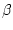 =
=  . Außerdem ist
. Außerdem ist
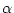 +
+ 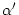 +
+ 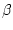 +
+  = 1800.
Also ist
2
= 1800.
Also ist
2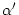 +2
+2 = 1800. Daher ist
= 1800. Daher ist
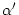 +
+  = 900.
= 900.
Zu 2.
Abbildung 3.6:
Umkehrung des Thalessatze
 |
Sei mb die Mittelsenkrechte der Seite [AC] M ist der Schnittpunkt von mb
mit [AB]. Dann ist
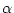 =
= 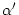 , da das Dreieck
, da das Dreieck
 AMC
gleichschenklig ist. Also ist
AMC
gleichschenklig ist. Also ist
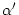 +
+  = 900 und es ist
= 900 und es ist
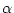 +
+ 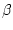 = 900. Also ist
= 900. Also ist
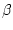 =
=  . Also ist
. Also ist
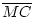 =
= 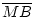 und damit
ist
und damit
ist
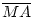 =
= 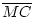 =
= 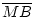 . Also liegen die drei Punkte
A, B, C auf einem Kreis um M mit Radius
. Also liegen die drei Punkte
A, B, C auf einem Kreis um M mit Radius
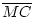 .
.

Definition 3.3.1
Die Lote von den Eckpunkten A, B, C eines Dreiecks auf die
gegenüberliegenden Seiten heißen Höhen des Dreiecks. hc ist das Lot
von C auf [AB]. hb ist das Lot von B auf [AC] und so weiter.
Abbildung 3.7:
Die Höhen
 |
Definition 3.3.2
Sei P ein Punkt der Geraden g. Ist F der Fußpunkt des Lotes von P
auf g, so heißt die Zahl
 Abstand von P zu g.
Abstand von P zu g.
Bemerkung 3.3.2
Auf jeder Seite der Geraden g gibt es eine Parallele im Abstand d. Die
Punkte auf dieser Parallelen sind genau die Punkte, die von g den
Abstand d haben.
Unterabschnitte
Andreas Bartholome
2003-11-28
![]()