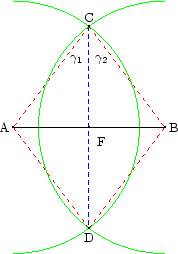
Gegeben ist eine Strecke [AB]. Konstruiere
eine Gerade, die senkrecht auf AB steht und durch die Mitte
von [AB] geht. Man sagt: Konstruiere die Mittelsenkrechte von
[AB].
Die Lösung sieht folgendermaßen aus:
- Zeichne k(A, r) mit
r >
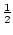
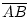 .
.
- Zeichne k(B, r) mit dem gleichen Radius r.
Die Verbindungsgerade der beiden Schnittpunkte ist die gesuchte
Mittelsenkrechte.
Begründung:
Nach Konstruktion ist
 DAC
DAC 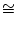
 DBC(SSS).
Also ist
DBC(SSS).
Also ist
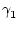 =
= 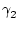 . Daher ist
. Daher ist
 DAF
DAF 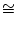
 DBF (SWS).
Also ist:
DBF (SWS).
Also ist:
-
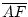 =
= 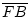 .
.
-
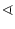 AFD =
AFD = 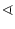 BFD. Und da außerdem
BFD. Und da außerdem
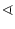 AFD +
AFD + 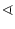 BFD = 1800 ist,
ist
BFD = 1800 ist,
ist
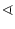 AFD = 900.
AFD = 900.
Andreas Bartholome
2003-11-28