Definition 3.3.1
f hat an der Stelle a ein lokales Maximum, wenn
es eine Umgebung
U (a) : {x|| x - a| <
(a) : {x|| x - a| < 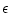 } gibt,
so dass für alle
x
} gibt,
so dass für alle
x 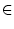 U
U (a) gilt:
f (x)
(a) gilt:
f (x)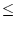 f (a).
Entsprechend erkärt man den Begriff des lokalen Minimums.
f (a).
Entsprechend erkärt man den Begriff des lokalen Minimums.
Satz 3.3.1
Es liege a im Innern des Definitionsbereiches von
f : 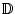
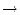
 .
Ist f an der Stelle a differnzierbar und hat f dort einen
lokalen Extremwert,
so ist f'(a) = 0.
.
Ist f an der Stelle a differnzierbar und hat f dort einen
lokalen Extremwert,
so ist f'(a) = 0.
Beweis:Sei (an) die Folge
(a +  ). Dann gilt:
). Dann gilt:


=
f'(
a).
Da f an der Stelle a einen lokales Maximum hat, sind fast alle
Folgenglieder 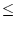 0. Also ist der Grenzwert
f'(a)
0. Also ist der Grenzwert
f'(a)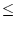 0.
Betrachte man die Folge
a -
0.
Betrachte man die Folge
a -  , so ergibt sich
f'(a)
, so ergibt sich
f'(a)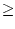 0. Zusammen ergibt sich, dass f'(a) = 0 ist.
0. Zusammen ergibt sich, dass f'(a) = 0 ist. 
Unterabschnitte
Andreas Bartholome
2003-11-26
 = f'(a).
= f'(a).