Unendliche Mengen
Auf einer Party tummeln sich eine Menge von Damen
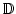 und eine Menge von
Herren
und eine Menge von
Herren
 . Es ist Damenwahl. Jede der Damen sucht sich einen Tänzer
aus. Und siehe da es bleibt keiner übrig. Die Damen sind sehr tanzfreudig und
so wird auch in den nächsten Runden keiner der noch so faulen Herren seinem
Schicksal entgehen. Mathematisch heißt dies: Es gibt eine bijektive Funktion
. Es ist Damenwahl. Jede der Damen sucht sich einen Tänzer
aus. Und siehe da es bleibt keiner übrig. Die Damen sind sehr tanzfreudig und
so wird auch in den nächsten Runden keiner der noch so faulen Herren seinem
Schicksal entgehen. Mathematisch heißt dies: Es gibt eine bijektive Funktion
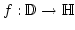 und jede injektive Funktion
und jede injektive Funktion
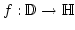 ist auch surjektiv. Das heißt
insbesondere ist jede injektive Funktion
ist auch surjektiv. Das heißt
insbesondere ist jede injektive Funktion
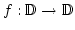 auch surjektiv.
1
auch surjektiv.
1
Er hat auch eine schöne Begründung dafür, dass es eine unendliche Menge gibt:
,, Meine Gedankenwelt, d.h. die Gesamtheit 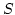 aller Dinge, welche
Gegenstand meines Denkens sein können, ist unendlich. Denn wenn
aller Dinge, welche
Gegenstand meines Denkens sein können, ist unendlich. Denn wenn 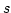 ein
Element von
ein
Element von 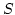 bedeutet, so ist der Gedanke s', dass
bedeutet, so ist der Gedanke s', dass 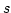 der Gegenstand
meines Denkens sein kann, selbst ein Element von S. Sieht man dasselbe als
Bild
der Gegenstand
meines Denkens sein kann, selbst ein Element von S. Sieht man dasselbe als
Bild
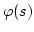 des Elementes
des Elementes 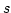 an, so hat daher die hierdurch bestimmte
Abbildung
an, so hat daher die hierdurch bestimmte
Abbildung 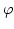 ...`` die gewünschten Eigenschaften.
...`` die gewünschten Eigenschaften.
Abbildung 7:
Gedanken
|
![\includegraphics[width=0.5\textwidth]{bilder/gedanken}](img221.png) |
Ich muss gestehen: Mich überzeugt der Beweis. Es gibt Beckmesser, die ihn
nicht schlüssig finden. Auf jeden Fall erhellt Dedekinds Definition auf
einmal schlaglichtartig, dass das Unendliche eigentlich näher liegt als das
endliche. Hilbert hat diese Definition durch sein schönes Bild vom Hilbert
Hotel erläutert.
Einer der Kritiker Dedekinds war sein Freund Georg Cantor. Er hatte übrigens
die etwas unangenehme Art die Freundschaft unter wissenschaftlichen
Auseinandersetzungen leiden zu lassen.
So schreibt er in einem Brief an Hilbert:
[HM91, Seite 427]
,,Dedekind geht offenbar von der Meinung aus, dass die Zahlentheorie keine
anderen Axiome voraussetze als die logischen; dasselbe scheinen die
Vertreter des Logikcalcüls zu glauben.
...
Mein anderer Gegensatz zu Dedekind besteht, wie Sie ja wissen, darin, dass er
jede bestimmte Vielheit für consistent hält, also den Unterschied von
consistenten und inconsistenten Vielheiten nicht zugiebt``
Dedekind definiert Unendlichkeit als Beziehung einer Menge zu sich. Nicht
durch die Elemente der Menge. Dedekind erklärt durch soziale Beziehungen die Unendlichkeit.
Satz 3.1
Folgende Aussagen sind äquivalent:
- Es gibt eine unendliche Menge.
- Es gibt eine freie zyklische einstellige Algebra.
Beweis:1.
 Es gibt eine unendliche Menge
Es gibt eine unendliche Menge  . Das heißt es gibt
eine injektive Abbildung
. Das heißt es gibt
eine injektive Abbildung
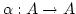 , welche nicht surjektiv
ist. Also ist
, welche nicht surjektiv
ist. Also ist
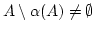 . Sei
. Sei ![$ [a]$](img223.png) die kleinste
Unteralgebra von
die kleinste
Unteralgebra von  , welche
, welche 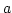 enthält.
enthält.
![$ ([a],\alpha)$](img224.png) ist dann eine freie
zyklische einstellige Algebra.
ist dann eine freie
zyklische einstellige Algebra.
2.
 1. Ist klar.
1. Ist klar. 
Hinweise:
- Der Begriff der Unendlichkeit überträgt sich von der Kategorie der Mengen ganz
leicht auf andere Kategorien. So kann man sagen: Ein Vektorraum
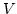 hat
unendliche Dimension, genau dann wenn es einen injektiven Homomorphismus gibt,
der nicht surjektiv ist. 3
hat
unendliche Dimension, genau dann wenn es einen injektiven Homomorphismus gibt,
der nicht surjektiv ist. 3
Erklärung 3.2
Ein Objekt  in einer Kategorie heißt unendlich, wenn es einen
Monomorphismus
in einer Kategorie heißt unendlich, wenn es einen
Monomorphismus
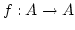 gibt, der kein Epimorphismus ist. Endlich
heißt
gibt, der kein Epimorphismus ist. Endlich
heißt  , wenn dies nicht der Fall ist.
, wenn dies nicht der Fall ist.
- In diesem Sinne in in der Kategorie der abelschen Gruppen
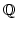
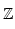 endlich, während
endlich, während
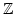 unendlich ist. Also etwas als Menge
größeres ist endlich. Dies zeigt einen weiteren Aspeckt der Definition von
Dedekind. Ob etwas endlich ist hängt von den Beziehungen ab, die möglich sind.
unendlich ist. Also etwas als Menge
größeres ist endlich. Dies zeigt einen weiteren Aspeckt der Definition von
Dedekind. Ob etwas endlich ist hängt von den Beziehungen ab, die möglich sind.
Man hätte auch den dualen Begriff nehmen können etwa
Erklärung 3.3
Ein Objekt  in einer Kategorie heißt kounendlich, wenn es einen
Epimorphismus
in einer Kategorie heißt kounendlich, wenn es einen
Epimorphismus
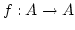 gibt, der kein Monomorphismus ist.
gibt, der kein Monomorphismus ist.
Satz 3.2
In der Kategorie der Mengen ist eine Menge genau dann unendlich, wenn sie
kounendlich ist.
Beweis:Sei 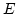 eine endliche Menge und
eine endliche Menge und
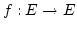 eine surjektive
Abbildung. Dann gibt es ein
eine surjektive
Abbildung. Dann gibt es ein
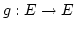 mit
mit 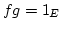 . Also ist
. Also ist 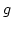 eine injektive Abbildung und als solche surjektiv weil
eine injektive Abbildung und als solche surjektiv weil 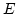 endlich ist.
Damit ist
endlich ist.
Damit ist 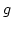 bijektiv und
bijektiv und 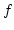 ist die Umkehrabbildung
ist die Umkehrabbildung 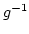 . Also ist
auch
. Also ist
auch 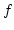 injektiv.
injektiv.
Ist umgekehrt 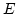 kounendlich und
kounendlich und
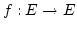 eine injektive
Funktion, so gibt es ein
eine injektive
Funktion, so gibt es ein
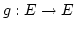 mit
mit 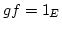 . Daher ist
. Daher ist 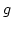 eine surjektive Funktion, die nach Voraussetzung injektiv ist. Daher ist
eine surjektive Funktion, die nach Voraussetzung injektiv ist. Daher ist 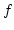 die Umkehrfunktion von
die Umkehrfunktion von 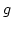 und als solche surjektiv. Also ist
und als solche surjektiv. Also ist 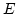 endlich.
endlich. 
Dieser Satz 3.2 gilt in anderen Kategorien nicht.
- Beispielsweise ist jeder unendliche Integritätsring, der nicht Körper
ist, in der Kategorie der Moduln über diesem Ring unendlich aber keineswegs
kounendlch.
-
![$ \mathbb{Z}[1/2]/\mathbb{Z}$](img235.png) ist in der Kategorie der abelschen Gruppen
kounendlich aber endlich.
ist in der Kategorie der abelschen Gruppen
kounendlich aber endlich.
Ab jetzt stellen wir uns auf den Standpunkt des heiligen Augustinus. Wir
glauben also an die Existenz einer unendlichen Menge. Wegen Satz ![[*]](file:/usr/share/latex2html/icons/crossref.png) gibt es dann eine freie einstellige zyklische Algebra.
Dedekind nennt sie in [Ded65, Seite 16] einfach unendlich.
Nach dem Basissatz
2.9 ist diese bis auf Isomorphie eindeutig bestimmt. Wir wählen
eine solche aus und nennen sie
gibt es dann eine freie einstellige zyklische Algebra.
Dedekind nennt sie in [Ded65, Seite 16] einfach unendlich.
Nach dem Basissatz
2.9 ist diese bis auf Isomorphie eindeutig bestimmt. Wir wählen
eine solche aus und nennen sie
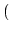
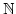
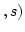 . Sie werde erzeugt von 0.
. Sie werde erzeugt von 0.
Satz 3.3
Eine einstellige Algebra ist genau dann zyklisch, wenn sie epimorphes Bild
von
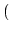
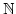
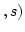 ist.
ist.
Beweis:Sei
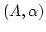 eine zyklische einstellige Algebra. Ein Element
eine zyklische einstellige Algebra. Ein Element 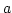 erzeugt
also
erzeugt
also  . Das heißt
. Das heißt ![$ [a]=A$](img237.png) . Wegen dem Rekursionsatz 2.8
gibt es zu der Abbildung
. Wegen dem Rekursionsatz 2.8
gibt es zu der Abbildung
![$ \{0\}\ni 0\mapsto a\in [a]=A$](img238.png) genau ein
Homomorphismus
genau ein
Homomorphismus
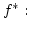
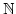
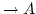 mit
mit
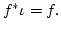
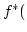
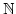
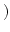 ist als epimorphes Bild einer abgeschlossenen Menge
abgschlossen. Also ist
ist als epimorphes Bild einer abgeschlossenen Menge
abgschlossen. Also ist
![$ A=[a]\subset f^{*}(N)$](img244.png) . Daher ist
. Daher ist 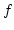 surjektiv. Die
Umkehrung ist einfach.
surjektiv. Die
Umkehrung ist einfach. 
Satz 3.4
Jede einstellige Algebra ist epimorphes Bild einer freien einstelligen Algebra.
Beweis:Sei 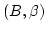 eine einstellige Algebra. Sie werde erzeugt von
eine einstellige Algebra. Sie werde erzeugt von 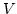 . Man
kann die elementfremde Vereinigung
. Man
kann die elementfremde Vereinigung
bilden. Als Funktion wählt man :
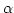 ist injektiv und nicht surjektiv. Die Elemente aus
ist injektiv und nicht surjektiv. Die Elemente aus
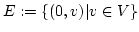 kommen nicht im Bild von
kommen nicht im Bild von 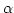 vor. Außerdem erzeugt
vor. Außerdem erzeugt 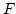 .
Also ist
.
Also ist 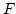 frei. Zu der Abbildung
frei. Zu der Abbildung
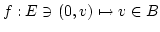 gibt es ein
eindeutig bestimmtes
gibt es ein
eindeutig bestimmtes
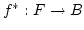 mit
mit
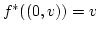 für alle
für alle
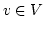 . Die Bildmenge von
. Die Bildmenge von 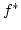 ist abgeschlossen in
ist abgeschlossen in 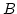 und enthält
und enthält
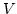 . Daher ist
. Daher ist 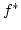 surjektiv.
surjektiv. 
Satz 3.5
- Jede Teilmenge einer endlichen Menge ist endlich.
- Ist
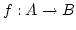 eine injektive Abbildung in eine endliche Menge
eine injektive Abbildung in eine endliche Menge
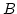 , so ist
, so ist  endlich.
endlich.
- Jedes epimorphe Bild einer endlichen Menge ist endlich.
- Die Vereinigung zweier endlicher Mengen ist endlich.
Beweis:Zu 1. Sei  eine Teilmenge der endlichen Menge
eine Teilmenge der endlichen Menge 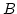 . Dann ist
. Dann ist
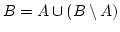 . Sei
. Sei
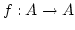 eine injektive Abbildung.
Wir erklären eine injektive Abbildung
eine injektive Abbildung.
Wir erklären eine injektive Abbildung
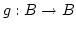 mit
mit 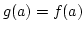 für
alle
für
alle 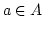 .
.
Behauptung: 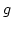 ist injektiv.
ist injektiv.
Es sei
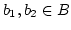 mit
mit
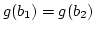 . Dann gibt es drei
Möglichkeiten:
. Dann gibt es drei
Möglichkeiten:
-
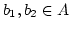 . Dann ist
. Dann ist
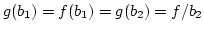 . Somit
ist
. Somit
ist
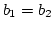 , da
, da 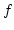 injektiv ist.
injektiv ist.
-
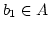 und
und
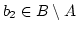 . Dann ist
. Dann ist
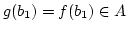 aber
aber
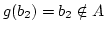 . Dann ist
. Dann ist
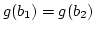 aber
unmöglich.
aber
unmöglich.
-
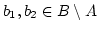 . Dann ist
. Dann ist
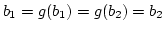 .
.
Also ist in jedem Fall, in dem
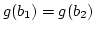 möglich ist, schon
möglich ist, schon
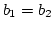 . Daher ist
. Daher ist 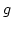 injektiv. Da
injektiv. Da 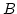 endlich ist, ist
endlich ist, ist 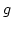 auch
surjektiv. Es gibt daher zu jedem
auch
surjektiv. Es gibt daher zu jedem 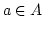 ein
ein 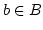 mit
mit 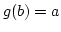 . Es ist
aber
. Es ist
aber
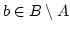 unmöglich. Denn dann wäre
unmöglich. Denn dann wäre
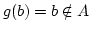 .
Andererseits
.
Andererseits 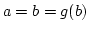 . Also ist
. Also ist 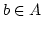 . Dann ist aber
. Dann ist aber 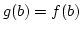 und man
hat: Zu jedem
und man
hat: Zu jedem 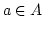 gibt es ein
gibt es ein 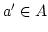 mit
mit 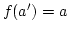 . Das heißt
. Das heißt  ist
surjektiv. Also ist
ist
surjektiv. Also ist  eine endliche Menge.
eine endliche Menge.
Zu 2. Man zeigt leicht, dass die Klasse der endlichen Mengen gegenüber
Bijektionen abgeschlossen ist. Damit folgt die Behauptung.
Zu 3. Ist
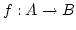 eine surjektive Abbildung mit endlichem
eine surjektive Abbildung mit endlichem  , so
gibt ein
, so
gibt ein
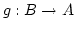 mit
mit 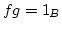 . Daher ist
. Daher ist 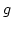 eine injektive
Abbildung.
eine injektive
Abbildung.
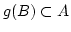 ist endlich. Daher ist
ist endlich. Daher ist 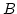 endlich.
endlich.

Andreas Bartholome
2005-03-06
![]() gibt, welche nicht surjektiv ist. Siehe [Ded65, Seite
13]2Entsprechen heißt eine Menge
gibt, welche nicht surjektiv ist. Siehe [Ded65, Seite
13]2Entsprechen heißt eine Menge ![]() endlich, wenn jede injektive Abbildung
endlich, wenn jede injektive Abbildung
![]() surjektiv ist.
surjektiv ist.aller Dinge, welche Gegenstand meines Denkens sein können, ist unendlich. Denn wenn
ein Element von
bedeutet, so ist der Gedanke s', dass
der Gegenstand meines Denkens sein kann, selbst ein Element von S. Sieht man dasselbe als Bild
des Elementes
an, so hat daher die hierdurch bestimmte Abbildung
...`` die gewünschten Eigenschaften.
![]() 1. Ist klar.
1. Ist klar. ![]()
![]() kounendlich und
kounendlich und
![]() eine injektive
Funktion, so gibt es ein
eine injektive
Funktion, so gibt es ein
![]() mit
mit ![]() . Daher ist
. Daher ist ![]() eine surjektive Funktion, die nach Voraussetzung injektiv ist. Daher ist
eine surjektive Funktion, die nach Voraussetzung injektiv ist. Daher ist ![]() die Umkehrfunktion von
die Umkehrfunktion von ![]() und als solche surjektiv. Also ist
und als solche surjektiv. Also ist ![]() endlich.
endlich. ![]()
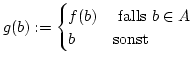
![]() mit
mit
![]() . Dann gibt es drei
Möglichkeiten:
. Dann gibt es drei
Möglichkeiten:
![]() eine surjektive Abbildung mit endlichem
eine surjektive Abbildung mit endlichem ![]() , so
gibt ein
, so
gibt ein
![]() mit
mit ![]() . Daher ist
. Daher ist ![]() eine injektive
Abbildung.
eine injektive
Abbildung.
![]() ist endlich. Daher ist
ist endlich. Daher ist ![]() endlich.
endlich.
![]()