Abbildung 6:
Rekursionssatz
|
![\includegraphics[width=0.8\textwidth]{bilder/morphismen.4}](img151.png) |
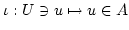 ist die Inklusionsabbildung.
ist die Inklusionsabbildung.
Erklärung 2.5
Sind die Voraussetzungen des Satzes erfüllt heißt
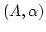 freie
einstellige Algebra mit Basis
freie
einstellige Algebra mit Basis 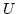 .
.
Beweis:Den Beweis des Satze habe ich dem entsprechenden Beweis im Buch
[Ea92, Seite15] nachempfunden.
Wir betrachten
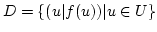 . Sie erzeugt eine kleinste
Untermenge
. Sie erzeugt eine kleinste
Untermenge ![$ [D]$](img156.png) in
in 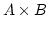 , die abgeschlossen gegenüber
, die abgeschlossen gegenüber
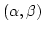 ist.
ist.
Beh: ![$ [D]$](img156.png) ist der Graph einer Funktion.
ist der Graph einer Funktion.
Bew:
- Zu jedem
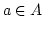 gibt es ein Paar
gibt es ein Paar
![$ (a,b)\in [D]$](img158.png) .
.
Beweis durch Induktion.
Sei 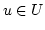 , dann ist
, dann ist 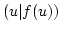 nach Definition in
nach Definition in ![$ [D]$](img156.png) . Sei
. Sei
Wir haben gesehen
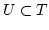 . Sei
. Sei 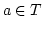 . Dann gibt es ein
. Dann gibt es ein 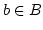 mit
mit
![$ (a\vert b)\in [D]$](img162.png) .
Daher ist
.
Daher ist
![$ (\alpha\times \beta)(a\vert b)\in [D]$](img163.png) , da
, da ![$ [D]$](img156.png) abgeschlossen
gegenüber
abgeschlossen
gegenüber
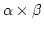 ist. Also ist
ist. Also ist
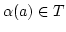 . Daher ist
. Daher ist 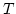 gegenüber
gegenüber 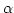 abgeschlossen. Daher ist
abgeschlossen. Daher ist 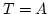 .
.
- Für jedes
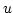 in
in 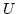 liegt nur
liegt nur 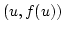 in
in ![$ [D]$](img156.png) .
.
Sei
![$ (u\vert f(u))\in [D]$](img167.png) mit
mit 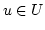 . Angenommen es gibt ein weiteres Paar
. Angenommen es gibt ein weiteres Paar
![$ (u\vert b)\in [D]$](img168.png) . Dann ist auch noch
. Dann ist auch noch
![$ [D]\setminus\{(u\vert b)\}$](img169.png) gegenüber
gegenüber
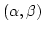 abgeschlossen. Dazu muss ich nur zeigen, dass
abgeschlossen. Dazu muss ich nur zeigen, dass 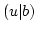 nicht als Bild eines Elementes aus
nicht als Bild eines Elementes aus
![$ [D]\setminus\{(u\vert b)\}$](img169.png) vorkommen kann.
Angenommen
vorkommen kann.
Angenommen
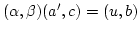 . Dann ist
. Dann ist
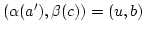 . Das bedeutet
. Das bedeutet
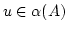 . Dies kann nach
Voraussetzung nicht sein. Also ist
. Dies kann nach
Voraussetzung nicht sein. Also ist
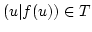 .
.
![$ [D]$](img156.png) ist rechtseindeutig. Beweis durch Induktion:
ist rechtseindeutig. Beweis durch Induktion:
Wieder sei
Zu zeigen bleibt  ist abgeschlossen gegenüber
ist abgeschlossen gegenüber 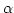 . Sei
. Sei
![$ (a,b)\in [D]$](img158.png) mit
mit 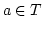 . Das heißt nur dieses
. Das heißt nur dieses 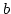 existiert, so dass
existiert, so dass
![$ (a,b)\in [D]$](img158.png) . Dann ist
. Dann ist
![$ (\alpha(a),\beta(b))\in [D]$](img179.png) . Angenommen es gibt
ein weiteres
. Angenommen es gibt
ein weiteres
![$ (\alpha(a),c)\in [D]$](img180.png) . Dann ist auch noch
. Dann ist auch noch
![$ [D]\setminus
\{(\alpha(a)\vert c)\}$](img181.png) gegenüber
gegenüber
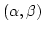 abgeschlossen. Denn
angenommen
abgeschlossen. Denn
angenommen
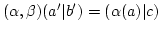 . Dann ist
. Dann ist
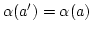 und daher (weil
und daher (weil 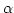 injektiv ist)
injektiv ist) 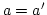 . Dann ist aber
. Dann ist aber
![$ (a,b')\in [D]$](img185.png) und
und
![$ (a,b)\in [D]$](img158.png) . Zu
. Zu 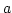 gab es nur ein
gab es nur ein 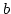 mit
mit
![$ (a,b)\in [D]$](img158.png) . Dann ist
. Dann ist 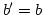 . Das heißt
. Das heißt
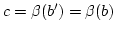 .
Dies widerspricht der Annahme
.
Dies widerspricht der Annahme
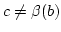 .
Also ist
.
Also ist ![$ [D]$](img156.png) der Graph einer Funktion und wegen Satz
der Graph einer Funktion und wegen Satz ![[*]](file:/usr/share/latex2html/icons/crossref.png) folgt die Behauptung.
folgt die Behauptung.
Wir sehen es war unbedingt wichtig, dass
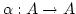 injektiv ist.
injektiv ist. 
Beweis:Sei 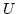 ein Basis von
ein Basis von  und
und 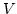 eine Basis von
eine Basis von 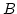 . Nach Voraussetzung
gibt es eine umkehrbare Abbildung
. Nach Voraussetzung
gibt es eine umkehrbare Abbildung
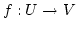 . Die Umkehrabbildung
sei
. Die Umkehrabbildung
sei 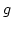 . Es gibt genau ein
. Es gibt genau ein
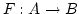 , so dass folgendes Diagramm
kommutativ ist.
, so dass folgendes Diagramm
kommutativ ist.
Genauso gibt es ein 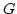 , so dass folgendes Diagramm kommutativ ist. , so dass folgendes Diagramm kommutativ ist.
|
Man erhält also
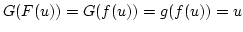 für alle
für alle 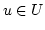 .
Andererseits ist
.
Andererseits ist
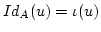 für alle
für alle 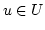 . Es gibt nur eine
solche Abbildung. Daher ist
. Es gibt nur eine
solche Abbildung. Daher ist 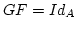 . genauso folgt
. genauso folgt 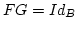 . Das war
aber behauptet.
. Das war
aber behauptet. 
So wie wir den Satz formuliert haben besteht eine völlige Analogie etwa zur
Theorie der Vektorräume oder der freien Moduln. Auf der Basis ist man frei
Homomorphismen zu definieren. Der definierte Homomorphismus ist dann auch
eindeutig. Es ist also sinnvoll eine einstellige Algebra
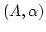 mit
Basis frei zu nennen.
mit
Basis frei zu nennen.
Hinweise:
- Ist in der Kategegorie der einstelligen
Abbildungen jeder Epimorphismus eine surjektive
Abbildung?
- Ist jeder Monomorphismus eine injektive Abbildung?
Beweis:Sei
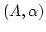 eine freie einstellige Algebra mit der Basis
eine freie einstellige Algebra mit der Basis
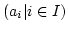 . Wir betrachten die Familie
. Wir betrachten die Familie
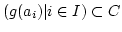 . Zu dieser
Familie gibt es nach dem Auswahlaxiom eine Familie
. Zu dieser
Familie gibt es nach dem Auswahlaxiom eine Familie
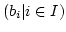 mit
mit
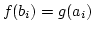 für alle
für alle 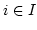 . Wir erklären
. Wir erklären
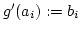 . Nach
dem Rekursionssatz gibt es einen eindeutigen bestimmten Homomorphismus
. Nach
dem Rekursionssatz gibt es einen eindeutigen bestimmten Homomorphismus
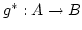 mit
mit
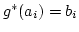 . Damit ist
. Damit ist
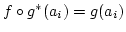 und damit
und damit
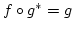 . Dies war zu zeigen.
. Dies war zu zeigen. 
Hinweise:
- Unteralgebren freier Algebren sind auch frei.
- Damit sind projektive Algebren frei.
Andreas Bartholome
2005-03-06
![]() . Sie erzeugt eine kleinste
Untermenge
. Sie erzeugt eine kleinste
Untermenge ![]() in
in ![]() , die abgeschlossen gegenüber
, die abgeschlossen gegenüber
![]() ist.
ist.
![]() ist der Graph einer Funktion.
ist der Graph einer Funktion.
![]() , dann ist
, dann ist ![]() nach Definition in
nach Definition in ![]() . Sei
. Sei
![]() mit
mit ![]() . Angenommen es gibt ein weiteres Paar
. Angenommen es gibt ein weiteres Paar
![]() . Dann ist auch noch
. Dann ist auch noch
![]() gegenüber
gegenüber
![]() abgeschlossen. Dazu muss ich nur zeigen, dass
abgeschlossen. Dazu muss ich nur zeigen, dass ![]() nicht als Bild eines Elementes aus
nicht als Bild eines Elementes aus
![]() vorkommen kann.
Angenommen
vorkommen kann.
Angenommen
![]() . Dann ist
. Dann ist
![]() . Das bedeutet
. Das bedeutet
![]() . Dies kann nach
Voraussetzung nicht sein. Also ist
. Dies kann nach
Voraussetzung nicht sein. Also ist
![]() .
.
![]() für alle
für alle ![]() .
Andererseits ist
.
Andererseits ist
![]() für alle
für alle ![]() . Es gibt nur eine
solche Abbildung. Daher ist
. Es gibt nur eine
solche Abbildung. Daher ist ![]() . genauso folgt
. genauso folgt ![]() . Das war
aber behauptet.
. Das war
aber behauptet. ![]()
![]() mit
Basis frei zu nennen.
mit
Basis frei zu nennen.
![$ \begin{array}[t]{ccc}
& & A \\
&\swarrow g^{*}& \Big \downarrow g\\
B&\mbo...
...aystyle \stackrel{f}{\mbox{$\makebox[3em]{\rightarrowfill}$}}$} &C
\end{array}$](img204.png)