Andere Kennzeichen der Unendlichkeit
Wir müssen etwas vorbereiten
Wir sagen ein 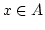 ist erreichbar von
ist erreichbar von 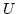 aus, wenn
aus, wenn ![$ x\in [U]$](img368.png) ist.
ist.
Hilfssatz 3.9
Ist
![$ \alpha:[a]\rightarrow [a]$](img369.png) surjektiv, so gilt für alle
surjektiv, so gilt für alle ![$ c\in [a]$](img370.png) :
:
![$ [c]=[a]$](img371.png)
Beweis:Sei
![$\displaystyle T=\{c\vert c\in [a]$](img372.png)
und
![$\displaystyle [c]=[a]\}$](img373.png)
Es ist 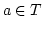 . Sei
. Sei 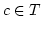 . Es
gilt
. Es
gilt
![$ [c]=\{c\}\cup \alpha([c])$](img375.png) . Ist
. Ist
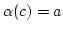 , so ist
, so ist
![$ [\alpha(c)]=[a]$](img377.png) und man ist fertig. Andernfalls gibt es ein
und man ist fertig. Andernfalls gibt es ein ![$ y\in [c]$](img378.png) mit
mit
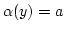 . Daher ist
. Daher ist
![$ \alpha(a)\in \alpha([c])=[\alpha(c)]$](img380.png) . Daher ist
. Daher ist
![$ [\alpha(a)]=[\alpha(c)]$](img381.png) . Nun ist aber
. Nun ist aber
![$ [\alpha(a)]=[a]$](img382.png) . Denn es gibt ein
. Denn es gibt ein
![$ y\in [a]$](img383.png) mit
mit
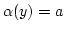 . Daher ist
. Daher ist
![$ a\in \alpha([a])=[\alpha(a)]$](img384.png) . Es
ist also
. Es
ist also
![$ [a]=[\alpha(a)]$](img385.png) . Wir können daher obige Gleichung
weiterschreiben.
. Wir können daher obige Gleichung
weiterschreiben.
![$ [\alpha(a)]=[\alpha(c)]=[a]$](img386.png) .
.  ist daher gegenüber
ist daher gegenüber
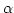 abgeschlossen. Es ist
abgeschlossen. Es ist ![$ T=[a]$](img75.png) .
. 
Beweis:Sei
Es ist 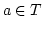 nach Voraussetzung. Sei
nach Voraussetzung. Sei
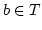 . Also
. Also
![$ b\notin[\alpha(b)]$](img391.png) . Angenommen
. Angenommen
![$ \alpha(b)\in
\alpha([\alpha(b)])=[\alpha(\alpha(b))]$](img392.png) . Es gibt dann ein
. Es gibt dann ein
![$ c\in
[\alpha(b)]$](img393.png) mit
mit
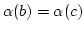 . Weil
. Weil 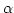 injektiv ist, ist
injektiv ist, ist
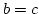 . Daher ist
. Daher ist
![$ b\in [\alpha(b)]$](img396.png) . Das ist ein Widerspruch zur
Voraussetzung.
. Das ist ein Widerspruch zur
Voraussetzung. 
Hilfssatz 3.11
Sei
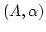 mit injektivem
mit injektivem 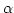 . Für
. Für 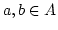 gilt:
gilt:
![$ [a]\cap
[b]=\emptyset$](img398.png) . oder
. oder
![$ [a]\subset [b]$](img399.png) oder
oder
![$ [b]\subset [a].$](img400.png)
Beweis:Wir betrachten
![$ [b]\setminus [a]$](img401.png) .
.
- Ist
![$ b\notin [a]$](img402.png) , so ist
, so ist ![$ b\in [a]$](img403.png) und daher
und daher
![$ [b]\subset [a]$](img404.png) . Man
ist fertig.
. Man
ist fertig.
- Andernfalls ist
![$ b\in [b]\setminus [a]=T$](img405.png) .
.
- Ist
![$ [b]\setminus [a]$](img401.png) abgeschlossen gegenüber
abgeschlossen gegenüber 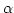 , so ist
, so ist
![$ [b]=[b]\setminus [a]$](img406.png) . Das heißt
. Das heißt
![$ [b]\cap [a]=\emptyset$](img407.png) .
.
-
![$ [b]\setminus [a]$](img401.png) ist nicht abgeschlossen gegenüber
ist nicht abgeschlossen gegenüber 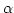 . Dann
gibt es ein
. Dann
gibt es ein
![$ c\in [b],c\notin[a]$](img408.png) , aber
, aber
![$ \alpha(c)\in [a]=\{a\}\cup
\alpha([a])$](img409.png) . Ist
. Ist
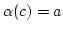 , so ist
, so ist
![$ [a]\subset [b]$](img399.png) und man ist
wieder fertig. Andernfalls ist
und man ist
wieder fertig. Andernfalls ist
![$ \alpha(c)\in \alpha([a])$](img410.png) . Es gibt daher
ein
. Es gibt daher
ein ![$ d\in [a]$](img411.png) mit
mit
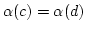 . Weil
. Weil 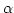 injektiv ist,
folgt
injektiv ist,
folgt 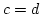 .Daher ist
.Daher ist ![$ c\in [a]$](img370.png) . Dies widerspricht der Wahl von
. Dies widerspricht der Wahl von 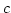 .
.

Beweis:Seien
![$ x,y\in [a]$](img56.png) mit
mit ![$ [x]=[y]$](img417.png) . Dann ist
. Dann ist ![$ x\in [y]$](img418.png) . Wäre
. Wäre 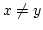 , so
wäre
, so
wäre
![$ x\in \alpha([y])$](img420.png) . Es gäbe ein
. Es gäbe ein
![$ c\in [y]=[x]$](img421.png) mit
mit
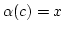 .
Dieses
.
Dieses 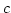 wäre auch in
wäre auch in ![$ [x]$](img423.png) . Das hieße
. Das hieße
![$ x\in \alpha([x])=[\alpha(x])$](img424.png) im
Widerspruch zum Lemma 3.10. Daher ist
im
Widerspruch zum Lemma 3.10. Daher ist 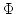 injektiv. Zu
zeigen bleibt die Surjektivität von
injektiv. Zu
zeigen bleibt die Surjektivität von 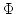 .
.
Sei 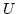 eine gegenüber
eine gegenüber 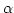 abgeschlossene Teilmenge von
abgeschlossene Teilmenge von ![$ [a]$](img223.png) . Ist
. Ist
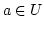 , so ist
, so ist ![$ [a]=U$](img427.png) und man ist fertig. Andernfalls ist
und man ist fertig. Andernfalls ist 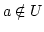 .
Sei
.
Sei
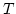 ist nicht gegenüber
ist nicht gegenüber 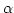 abgeschlossen, da
sonst
abgeschlossen, da
sonst ![$ T=[a]$](img75.png) , also
, also 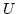 die leere Menge wäre. Also gibt es
die leere Menge wäre. Also gibt es 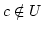 aber
aber
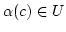 .
.
Beh.:
![$ [\alpha(c))]=U$](img432.png)
Bew.: Wäre das nicht der Fall, so gäbe es ein 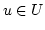 mit
mit
![$ u\notin[\alpha(c)]$](img433.png) . Also ist
. Also ist
![$ [u]\not\subset [\alpha(c)$](img434.png) und wegen
3 ist
und wegen
3 ist
![$ [u]\cap [\alpha(c)]\neq \emptyset$](img435.png) .
.
Angenommen
![$ u\notin[\alpha(c)]$](img433.png) , so ist
, so ist
![$ [\alpha(c)]\subset [u]$](img436.png) und
und
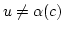 . Also ist
. Also ist
![$ \alpha(c)\in \alpha([u])$](img438.png) . Es gibt daher ein
. Es gibt daher ein ![$ d\in
[u]$](img439.png) mit
mit
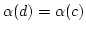 . Weil
. Weil 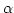 injektiv ist, ist
injektiv ist, ist 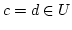 .
Das kann aber nicht sein. Es kann also ein
.
Das kann aber nicht sein. Es kann also ein
![$ u\in U\setminus[\alpha(c)]$](img442.png) nicht geben. Daher ist
nicht geben. Daher ist
![$ U=[\alpha(c)]$](img443.png) . Das heißt die Abbildung
. Das heißt die Abbildung 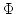 ist
surjektiv.
ist
surjektiv.

Beweis:1.
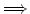 2.
2.
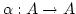 sei eine injektive nicht surjektive
Funktion und
sei eine injektive nicht surjektive
Funktion und
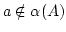 . Weiter sei
. Weiter sei ![$ [a]$](img223.png) die von
die von 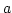 erzeugte
einstellige Unteralgebra. Ich betrachte die Menge der zyklischen
Unteralgebren von
erzeugte
einstellige Unteralgebra. Ich betrachte die Menge der zyklischen
Unteralgebren von ![$ [a]$](img223.png) . Durch
. Durch
![$\displaystyle \beta:[b]\mapsto [\alpha(b)]=\alpha([b])$](img449.png) |
(5) |
wird jeder solchen zyklischen Unteralgebra eine echte zyklische Unteralgebra
zugeordnet. Nach dem Rekursionssatz gibt es eine Funktion
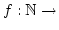
Menge der zyklischen Unteralgebren
mit
![$ f(0)=[a]$](img451.png) und
und
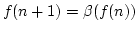 . (Dies kann man auch so formulieren: Es
gibt eine Funktion
. (Dies kann man auch so formulieren: Es
gibt eine Funktion
![$ g:[a]\rightarrow$](img453.png) Menge der zyklischen Unteralgebren mit
Menge der zyklischen Unteralgebren mit ![$ g(a)=[a]$](img454.png) und
und
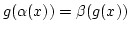 ) Beh.:
) Beh.: 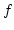 ist streng monoton
fallend.
ist streng monoton
fallend.
Bew: Es sei
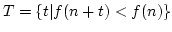 Es ist
Es ist ![$ f(n)=[b]$](img457.png) und
und
![$ f(n+1)=[\alpha(b)]\subsetneq [b]$](img458.png) . Also ist
. Also ist 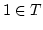 . Sei
. Sei 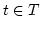 und
und
![$ f(n+t)=[b]$](img461.png) . Dann ist
. Dann ist
![$ f(n+t+1)=\beta([b])=[\alpha(b)\subsetneq
[b]=f(n+t)\subsetneq f(n)$](img462.png) . Also ist
. Also ist 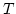 abgeschlossen gegenüber Nachfolgern.
Daher ist
abgeschlossen gegenüber Nachfolgern.
Daher ist
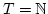 . Die Funktion
. Die Funktion 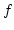 ist daher echt monoton fallend.
ist daher echt monoton fallend.
2.
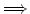 3.: Ist
3.: Ist
echt monoton
fallend, dann enthält
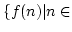
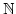
 kein minimales Element.
kein minimales Element.
3.
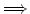 2. Sei
2. Sei
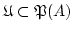 eine Menge ohne minimales
Element. Das bedeutet. Für jedes
eine Menge ohne minimales
Element. Das bedeutet. Für jedes
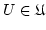 ist
ist
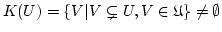 . Nach dem Auswahlaxiom gibt es daher
eine Funktion
. Nach dem Auswahlaxiom gibt es daher
eine Funktion
mit
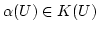 für
alle
für
alle
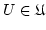 . Wir wählen ein beliebiges
. Wir wählen ein beliebiges
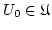 aus. Nach dem Rekursionssatz gibt es eine eindeutig bestimmte Funktion
aus. Nach dem Rekursionssatz gibt es eine eindeutig bestimmte Funktion
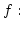
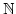
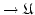 , mit
, mit
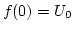 und
und
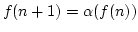 .
Man zeigt leicht:
.
Man zeigt leicht: 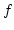 ist echt monoton fallend.
ist echt monoton fallend.
2.
 1. Da es eine streng monoton fallende Funktion
1. Da es eine streng monoton fallende Funktion
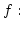
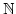
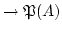 gibt, gibt es eine echt absteigende Kette
gibt, gibt es eine echt absteigende Kette
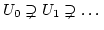 . Daher ist
. Daher ist
 eine Folge von nichtleeren paarweise
disjunkten Mengen. Nach dem Auswahlaxiom gibt es daher eine Folge
eine Folge von nichtleeren paarweise
disjunkten Mengen. Nach dem Auswahlaxiom gibt es daher eine Folge
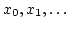 mit
mit
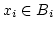 . Die
. Die 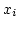 sind daher paarweise
verschieden. Wir haben daher eine injektive Funktion
sind daher paarweise
verschieden. Wir haben daher eine injektive Funktion
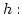
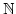
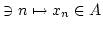 . Das heißt
. Das heißt  ist unendlich.
ist unendlich. 
Es ist natürlich auch  unendlich genau dann, wenn es Teilmenge von
unendlich genau dann, wenn es Teilmenge von
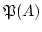 ohne maximales Element gibt.
Es müsste auch gezeigt werden können:
ohne maximales Element gibt.
Es müsste auch gezeigt werden können:  ist unendlich genau dann wenn es
eine Funktion
ist unendlich genau dann wenn es
eine Funktion
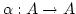 gibt und eine Bahn ohne Wiederkehr.
Dies
ist deutlich zu machen.
gibt und eine Bahn ohne Wiederkehr.
Dies
ist deutlich zu machen.
Satz 3.14
Ist  eine endliche Menge und
eine endliche Menge und 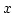 beliebig, so ist
beliebig, so ist
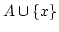 endlich.
endlich.
Beweis:Angenommen es gibt eine injektive Funktiopn
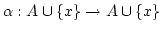 , welche nicht surjektiv ist. Also gibt es ein
, welche nicht surjektiv ist. Also gibt es ein
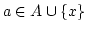 mit
mit
![$ [a]\cong$](img487.png)
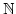 , welche nicht surjektiv ist.
, welche nicht surjektiv ist.
1. Fall:
![$ x\notin [a]$](img488.png) . Dann ist
. Dann ist
![$ [a]\subset A$](img489.png) und daher
und daher  unendlich.
unendlich.
2. Fall: Dann ist aber
![$ x\notin [\alpha(x))]\subset A$](img490.png) . Es ist aber auch
. Es ist aber auch
![$ [\alpha(x)]\cong$](img491.png)
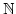 . Also ist wieder
. Also ist wieder  unendlich. Dies widerspricht
der Voraussetzung.
unendlich. Dies widerspricht
der Voraussetzung. 
Wir wollen eine Menge zählbar nennen, wenn es ein
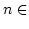
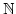 gibt und eine
Bijektion
gibt und eine
Bijektion
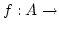
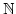
![$ \setminus [n]=\overline{[n]}$](img494.png) , wenn es also
eine Bijektion auf einen unteren Abschnitt von
, wenn es also
eine Bijektion auf einen unteren Abschnitt von
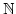 gibt.
gibt.
Satz 3.15
Eine Menge ist genau dann endlich, wenn sie zählbar ist.
Dies ist vielleicht das Endlichkeitskriterium welches den meisten Leuten
zuerst einfällt.
Beweis:Sei  endlich. Dann enthält die Menge der zählbaren Teilmengen von
endlich. Dann enthält die Menge der zählbaren Teilmengen von  ein
maximales Element
ein
maximales Element 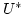 und eine bijektive Funktion
und eine bijektive Funktion
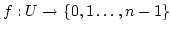 .
.
Beh. 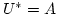 .
Wäre dies nicht der Fall, so gäbe es ein
.
Wäre dies nicht der Fall, so gäbe es ein 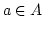 aber
aber
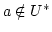 .
Wir betrachten
.
Wir betrachten
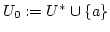 .
und die Funktion:
.
und die Funktion:
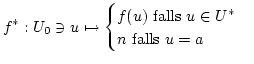 |
(6) |
Diese Funktion ist bijektiv. Das geht aber nicht, da schon 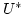 maximal
war.
maximal
war.
Zu zeigen oist, dass jeder untere Abschnitt von
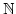 endlich ist.
Dies ist sicher richtig für
endlich ist.
Dies ist sicher richtig für
![$ \{0\}=\overline{[1]}$](img501.png) .
Sei
.
Sei
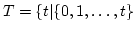 endlich endlich 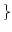 |
|
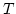 ist wegen 3.14 gegenüber Nachfolgern abgeschlossen
also ist
ist wegen 3.14 gegenüber Nachfolgern abgeschlossen
also ist
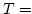
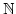 .
. 
Wir haben also folgendes Ergebnis. Die endlichen Mengen sind genau die Mengen,
die einem unteren Abschnitt von
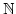 gleichmächtig sind.
Jetzt ist einfach:
gleichmächtig sind.
Jetzt ist einfach:
Satz 3.16
Die Vereinigung zweier endlicher Mengen ist endlich.
Hinweise:
- Ein Argument von Aristoteles:Zitiert nach ,,Aristoteles Kritiker der
Wirklichkeit`` [LL55, Seite 25]
,,Man kann behaupten, dass in jeglichem Bereiche, wo es eine Stufenreihe,
ein Höher oder Niedriger bezüglich der Vollkommenheit gibt, notwendig auch
ein schlechthin Vollkommenstes besteht. Da es nun unter dem, was ist, eine
solche Abstufung von Dingen höherer und geringerer Vollkommenheit gibt, so
gibt es auch ein vollkommenstes Seiendes, und dies dürfte das Göttliche
sein.``
Diese Bemerkung des Aristoteles erscheint falsch. Denn nehmen wir die Menge
der natürlichen Zahlen. Diese Menge ist der Größe nach geordnet aber sie
enthält kein größtes Element. Analog ist dies mit dem unendlichen Abstieg.
Auch
er ist nicht notwendig widersprüchlich. Im übrigen ist hier schon drin
enthalten, dass alle Mengen endlich sind. Denn sei
 eine unendliche
Menge. Dann enthält
eine unendliche
Menge. Dann enthält
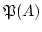 eine Teilmengeohne größtes Element. Ja
eine Teilmengeohne größtes Element. Ja
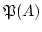 enthält sogar Ketten ohne größtes Element und Ketten ohne
kleinstes Element. Es ist aber die Frage, ob Aristoteles dies als
Gegenargument zugelassen hätte. Denn in einem anderen Sinne stimmt seine
Behauptung in der Potenzmenge schon. Und zwar wenn es nur endliche Mengen
gibt. Vielleicht ist das der geheime Grund warum er nur endliche Mengen
zulässt. Seine Gottesbeweise funktionieren sonst nicht.
enthält sogar Ketten ohne größtes Element und Ketten ohne
kleinstes Element. Es ist aber die Frage, ob Aristoteles dies als
Gegenargument zugelassen hätte. Denn in einem anderen Sinne stimmt seine
Behauptung in der Potenzmenge schon. Und zwar wenn es nur endliche Mengen
gibt. Vielleicht ist das der geheime Grund warum er nur endliche Mengen
zulässt. Seine Gottesbeweise funktionieren sonst nicht.
- Thomas von Aquin scheint explizit die Existenz der Unendlichkeit zu
leugnen. So schreibt er in der Summe wider die Heiden
[von74, 20. Kapitel ,,Gott ist kein Körper`` Seite 77]
,,Eine unendliche Größe gibt es nicht``
Andreas Bartholome
2005-03-06
![]() ist erreichbar von
ist erreichbar von ![]() aus, wenn
aus, wenn ![]() ist.
ist.
![]() eine gegenüber
eine gegenüber ![]() abgeschlossene Teilmenge von
abgeschlossene Teilmenge von ![]() . Ist
. Ist
![]() , so ist
, so ist ![]() und man ist fertig. Andernfalls ist
und man ist fertig. Andernfalls ist ![]() .
Sei
.
Sei
![]()
![]() mit
mit
![]() . Also ist
. Also ist
![]() und wegen
3 ist
und wegen
3 ist
![]() .
.
![]() , so ist
, so ist
![]() und
und
![]() . Also ist
. Also ist
![]() . Es gibt daher ein
. Es gibt daher ein ![]() mit
mit
![]() . Weil
. Weil ![]() injektiv ist, ist
injektiv ist, ist ![]() .
Das kann aber nicht sein. Es kann also ein
.
Das kann aber nicht sein. Es kann also ein
![]() nicht geben. Daher ist
nicht geben. Daher ist
![]() . Das heißt die Abbildung
. Das heißt die Abbildung ![]() ist
surjektiv.
ist
surjektiv.
![]()
![]() Es ist
Es ist ![]() und
und
![]() . Also ist
. Also ist ![]() . Sei
. Sei ![]() und
und
![]() . Dann ist
. Dann ist
![]() . Also ist
. Also ist ![]() abgeschlossen gegenüber Nachfolgern.
Daher ist
abgeschlossen gegenüber Nachfolgern.
Daher ist
![]() . Die Funktion
. Die Funktion ![]() ist daher echt monoton fallend.
ist daher echt monoton fallend.
![]() 3.: Ist
3.: Ist
![]() 2. Sei
2. Sei
![]() eine Menge ohne minimales
Element. Das bedeutet. Für jedes
eine Menge ohne minimales
Element. Das bedeutet. Für jedes
![]() ist
ist
![]() . Nach dem Auswahlaxiom gibt es daher
eine Funktion
. Nach dem Auswahlaxiom gibt es daher
eine Funktion
![]() 1. Da es eine streng monoton fallende Funktion
1. Da es eine streng monoton fallende Funktion
![]()
![]()
![]() gibt, gibt es eine echt absteigende Kette
gibt, gibt es eine echt absteigende Kette
![]() . Daher ist
. Daher ist
![]() eine Folge von nichtleeren paarweise
disjunkten Mengen. Nach dem Auswahlaxiom gibt es daher eine Folge
eine Folge von nichtleeren paarweise
disjunkten Mengen. Nach dem Auswahlaxiom gibt es daher eine Folge
![]() mit
mit
![]() . Die
. Die ![]() sind daher paarweise
verschieden. Wir haben daher eine injektive Funktion
sind daher paarweise
verschieden. Wir haben daher eine injektive Funktion
![]()
![]()
![]() . Das heißt
. Das heißt ![]() ist unendlich.
ist unendlich. ![]()
![]() unendlich genau dann, wenn es Teilmenge von
unendlich genau dann, wenn es Teilmenge von
![]() ohne maximales Element gibt.
Es müsste auch gezeigt werden können:
ohne maximales Element gibt.
Es müsste auch gezeigt werden können: ![]() ist unendlich genau dann wenn es
eine Funktion
ist unendlich genau dann wenn es
eine Funktion
![]() gibt und eine Bahn ohne Wiederkehr.
Dies
ist deutlich zu machen.
gibt und eine Bahn ohne Wiederkehr.
Dies
ist deutlich zu machen.
![]() . Dann ist
. Dann ist
![]() und daher
und daher ![]() unendlich.
unendlich.
![]() . Es ist aber auch
. Es ist aber auch
![]()
![]() . Also ist wieder
. Also ist wieder ![]() unendlich. Dies widerspricht
der Voraussetzung.
unendlich. Dies widerspricht
der Voraussetzung. ![]()
![]()
![]() gibt und eine
Bijektion
gibt und eine
Bijektion
![]()
![]()
![]() , wenn es also
eine Bijektion auf einen unteren Abschnitt von
, wenn es also
eine Bijektion auf einen unteren Abschnitt von
![]() gibt.
gibt.
![]() .
Wäre dies nicht der Fall, so gäbe es ein
.
Wäre dies nicht der Fall, so gäbe es ein ![]() aber
aber
![]() .
Wir betrachten
.
Wir betrachten
![]() .
und die Funktion:
.
und die Funktion:
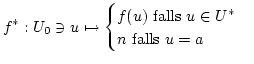
![]() endlich ist.
Dies ist sicher richtig für
endlich ist.
Dies ist sicher richtig für
![]() .
Sei
.
Sei