Ergänzungen zur ägyptischen Multiplikation
Auf der Seite 4 des Büchleins wird die ägyptische Multiplikation
besprochen. Natürlich
geht der Beweis, dass das ägyptische Verfahren richtig ist, auch ,,von unten``.
Sei
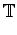
= {
b|
a . k =
aemul (
a,
k) für alle
k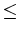 b
b}
Es ist
0 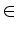
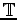 . Sei
b
. Sei
b 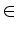
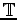 . Wir betrachten b + 1.
. Wir betrachten b + 1.
1.Fall:
b + 1 = 2 . s ist gerade. Dann ist
s = (b + 1)/2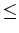 b. Daher ist
aemul (a, b) = aemul (a, 2 . s) = aemul (a . 2, s) = (a . 2)s = a . (2s) = a . (b + 1).
b. Daher ist
aemul (a, b) = aemul (a, 2 . s) = aemul (a . 2, s) = (a . 2)s = a . (2s) = a . (b + 1).
2. Fall: b + 1 ist ungerade. Dann ist
aemul (a, b + 1) = aemul (a, b) + a = a . b + a = a(b + 1). Also gehört in jedem Fall b + 1 zu
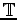 . Es ist daher
. Es ist daher
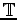 induktiv und somit gleich
induktiv und somit gleich
 .
.
Die ägyptische Multiplikation soll in Lisp programmiert werden.
Die Funktion ergibt t, wenn x gerade ist, andernfalls nil.
Entsprechend gibt diese Funktion t, wenn x ungerade ist.
(defun aemulr(a b)
(if (= b 0) 0
(if (= (mod b 2) 0) (aemulr (* a 2) (/ b 2))
(+ (aemulr a (- b 1)) a))))
(aemulr 33 1234) ===> 40722
Die Funktion ist rekursiv definiert, die Definition ist genau dem Beweis aus
dem Büchlein nachvollzogen.
- Ist b = 0, so wird 0 zurückgegeben.
- Ist b gerade, so wird die Funktion aemulr mit den Argumenten
a . 2 und b/2 aufgerufen.
- Ist b ungerade, so wird die Funktion mit den Argumenten a, b - 1
aufgerufen und a dazu addiert. Also
a + aemul (a, b - 1).
Diese Art der Programmierung kann wörtlich für Common Lisp übernommen
werden. Die Multiplikation von a mit 2 kann durch a + a
ersetzt werden.
Verfolgt man, wie die verschiedenen Aufrufe in die Tiefe gehen, versteht man
vielleicht besser wie die Funktion arbeitet.
(aemulr 67 3)
1 -> aemulr: a=67 b=3
| 2 -> aemulr: a=67 b=2
| | 3 -> aemulr: a=134 b=1
| | | 4 -> aemulr: a=134 b=0
| | | 4 <- aemulr: 0
| | 3 <- aemulr: 134
| 2 <- aemulr: 134
1 <- aemulr: 201
Ich möchte dies genau erklären:
- Die Funktion wird aufgerufen mit den Argumenten a = 67 und b = 3.
- Da b
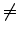 0 ist, und b ist wird aemulr mit den Argumenten
67 und 2 aufgerufen. Auf dieser zweiten Stufe wird sich
a = 67 zum Addieren gemerkt. Wir erhalten den Term
67 + aemul (67, 2).
0 ist, und b ist wird aemulr mit den Argumenten
67 und 2 aufgerufen. Auf dieser zweiten Stufe wird sich
a = 67 zum Addieren gemerkt. Wir erhalten den Term
67 + aemul (67, 2).
- Wieder ist b
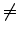 0 und infolgedessen wird die Funktion zum dritten Mal
aufgerufen. Diesmal weil b gerade ist mit den Argumenten 134 und 1.
Wir erhalten den Term
67 + aemul (134, 1).
0 und infolgedessen wird die Funktion zum dritten Mal
aufgerufen. Diesmal weil b gerade ist mit den Argumenten 134 und 1.
Wir erhalten den Term
67 + aemul (134, 1).
- Das zweite Argument ist wieder ungerade. Also wird die Funktion auf der
4ten Stufe wieder aufgerufen mit den Argumenten a = 134 und b = 0.
Wir erhalten den Term
67 + 134 + aemul (134, 0).
- Im 5ten Aufruf ist b = 0. Es wird das erste Argument 0 auf die 4te
Stufe zurückgegeben. Da sich dort 134 gemerkt wurde wird zu 0 die 134
dazu addiert und das Ergebnis auf die 3te Stufe nach oben durchgereicht. Dort
wurde sich nichts gemerkt. Also einfach auf die 2te Stufe. Dort liegt 67
zum Addieren bereit.
- Auf der ersten Stufe wird dann 201 ausgegeben.
Dies Verfahren ist nicht ganz einfach zu verstehen. Man sollte es sich durch
Listen nochmal klarer machen.
Zu den Beispielen im Buch:
(aemulr 32 31) 992
(aemulr 31 32) 992
(aemulr 17 17) 289
(aemulr 111 1231) 136641
(aemulr 3 63) 189
(aemulr 3 7)
1 -> aemulr: a=3 b=7
| 2 -> aemulr: a=3 b=6
| | 3 -> aemulr: a=6 b=3
| | | 4 -> aemulr: a=6 b=2
| | | | 5 -> aemulr: a=12 b=1
| | | | | 6 -> aemulr: a=12 b=0
| | | | | 6 <- aemulr: 0
| | | | 5 <- aemulr: 12
| | | 4 <- aemulr: 12
| | 3 <- aemulr: 18
| 2 <- aemulr: 18
1 <- aemulr: 21
Aber
(aemulr 7 3)
1 -> aemulr: a=7 b=3
| 2 -> aemulr: a=7 b=2
| | 3 -> aemulr: a=14 b=1
| | | 4 -> aemulr: a=14 b=0
| | | 4 <- aemulr: 0
| | 3 <- aemulr: 14
| 2 <- aemulr: 14
1 <- aemulr: 21
Man sieht daher, dass der Aufwand keineswegs kommutativ ist.
Bei diesem Verfahren ist es unschön, dass beim Aufsteigen weiter gerechnet
werden muss. Besser wäre es, wenn man schon auf der untersten Stufe das
Ergebnis hätte. Es könnte unverändert nach oben durchgereicht werden. Man
nennt dies endrekursiv.
Eine bessere Verwirklichung dieser Art der Multiplikation ist daher:
1 -> russ: p=0 a=33 b=5
| 2 -> russ: p=33 a=33 b=4
| | 3 -> russ: p=33 a=66 b=2
| | | 4 -> russ: p=33 a=132 b=1
| | | | 5 -> russ: p=165 a=132 b=0
| | | | 5 <- russ: 165
| | | 4 <- russ: 165
| | 3 <- russ: 165
| 2 <- russ: 165
1 <- russ: 165
(defun russ(p a b)
(if (= b 0) p
(if (= (mod b 2) 0) (russ p (+ a a) (/ b 2))
(russ (+ p a) a (1- b))
)))
Wir sehen: Hier ist das Ergebnis auf der tiefsten Stufe ausgerechnet. Es
braucht nur noch nach oben durchgereicht werden.
Aufgaben:
- Eine Funktion
ae :
 ×
×
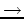
 wird
folgendermaßen definiert:
wird
folgendermaßen definiert:
- ae(a, 0) = p mit festem
p
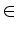
 für alle
a
für alle
a 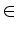
 .
.
- Ist b gerade, so ist
ae(a, b) = ae(a + a, b/2).
- Ist b ungerade so ist
ae(a, b) = a + ae(a, b - 1).
Gebe einen Term für ae(a, b) für alle
a, b 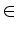
 an. Beweise, dass
dieser Term tatsächlich die Funktion ae(a, b) beschreibt.
an. Beweise, dass
dieser Term tatsächlich die Funktion ae(a, b) beschreibt.
- Eine Funktion
f :
 ×
×
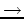
 heiße ägyptisch,
wenn sie die folgenden zwei Eigenschaften hat:
heiße ägyptisch,
wenn sie die folgenden zwei Eigenschaften hat:
-
f (a, b)) = f (a + a, b/2), falls b gerade ist.
-
f (a, b) = a + f (a, b - 1) falls b ungerade ist.
- Gibt es eine kommutative ägyptische Abbildung
f :
 ×
×
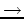
 mit f (1, 0) = 1 und f (3, 0) = 2?
mit f (1, 0) = 1 und f (3, 0) = 2?
- Zeige Ist f ägyptisch, so ist für alle
n
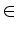
 :
f (0, n) = f (0, 0).
:
f (0, n) = f (0, 0).
- Kennzeichne alle kommutative ägyptischen Abbildungen
f
 ×
×
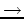
 .
.
- Kennzeichne alle ägyptischen Funktionen
f :
 ×
×
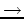
 . Ich weiß keine Antwort
. Ich weiß keine Antwort
- Kennzeichne alle ägyptischen Funktionen
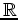 ×
×
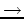
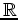 . Auch hier weiß ich keine Antwort.
. Auch hier weiß ich keine Antwort.
- Wir wollen den Begriff verallgemeinern:
Sei M eine beliebige nicht leere Menge. und
o: M×M
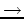 M eine Funktion. Wir wollen das Zeichen o zwischen die Argumente
schreiben. Also anstelle
o(a, b) = aob
Eine Funktion
f : M×
M eine Funktion. Wir wollen das Zeichen o zwischen die Argumente
schreiben. Also anstelle
o(a, b) = aob
Eine Funktion
f : M×
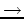 M heißt ägyptisch, wenn gilt:
M heißt ägyptisch, wenn gilt:
-
f (m, b) = f (mom, b/2) für alle m
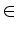 M und alle geraden
b
M und alle geraden
b 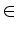
 .
.
-
f (m, b) = f (m, b - 1)om für alle ungeraden
b
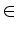
 .
.
- Was ergibt sich, wenn man die Menge
M =
 wählt und als
Verknüpfung o die Multiplikation?
wählt und als
Verknüpfung o die Multiplikation?
- Es sei
M =
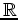 und
o:
und
o: 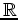 ×
×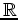
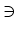 (a, b)
(a, b) 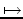
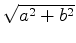
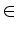
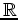 .
.
- Es sei
M =
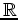 und
o:
und
o: 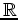 ×
×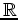
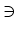 (a, b)
(a, b) 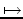 (a + b)/2
(a + b)/2 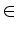
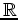 . Was ergibt sich?
. Was ergibt sich?
- Wähle
M =
 und
o:
und
o:  ×
×
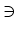 (a, b)
(a, b) 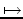 ab
ab 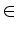
 .
.
- Es sei f (a, 0) = 1 für alle a. Berechne f (3, 6).
- Berechne f (5, 5).
Lösungen:
- 1
- Behauptung: Für alle
a, b
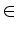
 ist
ae(a, b) = p + a . b.
ist
ae(a, b) = p + a . b.
Beweis: Es ist für alle a
ae(a, 0) = p = p + a . 0. Für b = 1 und beliebiges
a erhält man
ae(a, 1) = a + ae(a, 0) = a + p = p + a . 1. Es sei
T = {b| ae(a, k) = p + a . k für allea 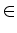 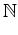 und allek und allek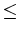 b} b} |
|
Wir haben gerade nachgerechnet, dass 0 und 1 in T sind.
Sei b 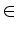 T. Wir betrachten nun b + 1.
T. Wir betrachten nun b + 1.
1. Fall:
b + 1 = 2 . s ist gerade. Dann ist
ae(a, 2s) = ae(a . 2, s) = p + a . 2 . s = p + a . (b + 1).
2. Fall: b + 1 ist ungerade.
ae(a, b + 1) = a + ae(a, b) = a + p + a . b = p + a . (b + 1)
Daher ist T induktiv und die Behauptung folgt für alle b.
- 2
- 2a
- Antwort: Nein. Denn Angenommen f ist eine solche
kommutative ägyptische Abbildung. Dann ist insbesonders
f (0, 3) = 0 + f (0, 2) = f (0, 1) = 0 + f (1, 0) = 1. Andererseits sollte f (3, 0) = 2
sein. Dies widerspricht sich.
Ich weiß noch nicht ob es überhaupt solche ägyptischen Abbildungen
gibt
Andreas
2006-12-05
![]() b. Daher ist
aemul (a, b) = aemul (a, 2 . s) = aemul (a . 2, s) = (a . 2)s = a . (2s) = a . (b + 1).
b. Daher ist
aemul (a, b) = aemul (a, 2 . s) = aemul (a . 2, s) = (a . 2)s = a . (2s) = a . (b + 1).
![]() . Es ist daher
. Es ist daher
![]() induktiv und somit gleich
induktiv und somit gleich
![]() .
.