Transversalen im Dreieck
Wie wir wissen schneiden sich die Mittelsenkrechten eines jeden Dreiecks im
Umkreismittelpunkt. Genauso schneiden sich die Winkelhalbierenden im
Inkreismittelpunk. Für die Höhen gilt ein ähnlicher Satz.
Satz 3.4.1
In jedem Dreick schneiden sich die Höhen in einem Punkt.
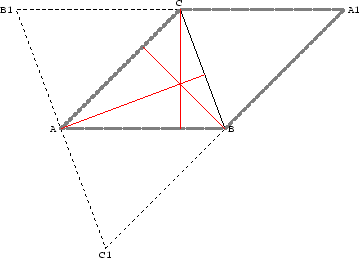
Beweis:Wir ziehen durch jeden Eckpunkt des Dreiecks
 ABC
eine Parallele zur gegenüberliegenden Seite. Es entsteht ein neues Dreieck
ABC
eine Parallele zur gegenüberliegenden Seite. Es entsteht ein neues Dreieck
 A1B1C1
A1B1C1
Abbildung 3.10:
Höhenschnittpunkt
 |
Es ist
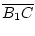 =
= 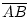 , da ABCB1 ein Parallelogramm
ist.
Genauso ist
, da ABCB1 ein Parallelogramm
ist.
Genauso ist
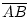 =
= 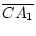 , da ABA1C ein
Parallelogramm ist. Also ist C der Mittelpunkt von
[B1A1]. Genauso
ist B der Mittelpunkt von
[C1A1] und A der Mittelpunkt von
[B1C1].
Die Mittelsenkrechten dieses neuen DReiecks
, da ABA1C ein
Parallelogramm ist. Also ist C der Mittelpunkt von
[B1A1]. Genauso
ist B der Mittelpunkt von
[C1A1] und A der Mittelpunkt von
[B1C1].
Die Mittelsenkrechten dieses neuen DReiecks
 A1B1C1
schneiden sich in einem Punkt. Die Mittelsenkrechten sind die Höhen in dem
ursprünglichen Dreieck
A1B1C1
schneiden sich in einem Punkt. Die Mittelsenkrechten sind die Höhen in dem
ursprünglichen Dreieck
 ABC.
Also schneiden sich die Höhen in einem Punkt, dem Höhenschnittpunkt.
ABC.
Also schneiden sich die Höhen in einem Punkt, dem Höhenschnittpunkt.

Verbindet man etwa die Seitenmitten von [BC] und [AC], so stellt man fest,
dass diese Gerade parallel zu AB ist.
Satz 3.4.2
Sei ein Dreieck ABC gegeben. Die Parallele durch die Seitenmitte E von
[AC]
zu der Seite AB geht durch die Seitenmitte von [BC].
Die Verbindungsstrecke der Schnittpunkte ist halbso lang wie [AB].
Beweis:
Abbildung 3.11:
Mittelparallele
 |
Zu zeigen ist: D ist die Seitenmitte von [BC]. Sei h die Parallele zu
[CB] ducrh E. Dann gilt:
- Das Dreieck AFE ist kongruent zu dem Dreieck EDC. Daher ist [EF]
genauso lang wie [CD].
- Das Viereck FBDE ist ein Parallelogramm. Also ist die Strecke [EF]
genauso lang, wie die Strecke [DE].
Daher ist [CD] genauso lang wie [DB]. Das bedeutet: D ist
Seitenmitte vonm [CD]. Genauso folgt, dass F Seitenmitte von [AB]
ist. Und daher ist die Strecke [ED]
0.5 . c lang. 
Folgerung 3.4.3
Verbindet man die Seitennmitten zweier Seiten, so ist diese Gerade parallel
zur dritten Dreiecksseite.
Überlege den Beweis dieses Satzes selbstständig.
Satz 3.4.4
Die Seitenhalbierenden eines jeden DReiecks schneiden sich in einem
Punkt. Dieser Punkt heißt Schwerpunkt des Dreiecks.
Ist S der Schwerpunkt des Dreiecks so gilt:
Die Länge von
[AS] = 2/3sa, die Länge von
BS = 2/3sb
und die Länge von
[CS] = 2/3sc.
Beweis:
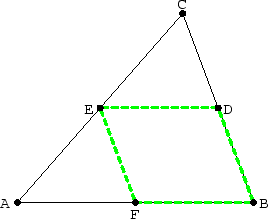
Abbildung 3.12:
Schwerpunkt
 |
In der Figur ist P die Seitenmitte von [AS] und Q die Seitenmitte von
[BS]. Entsprechend ist Mb die Seitenmitte von b
und Ma die Seitenmitte von a. Also ist wegen der Folgerung
3.4.3
das Viereck PQMaMb ein Viereck mit zwei gleichlangen gegenüberliegenden
Seiten. Daher ist es ein Parallelogramm und die Dieagonalen halbieren
sich. Also ist [PS] genauso lang wie [SMa]. Da P weiterhin die
Seitenmitte von [AS] ist. Also ist [AS]
2/3 . sa lang.
Ist S' der Schnittpunkt der Seitenhalbierenden sa und sc, so folgt
genauso, dass [AS']
2/3 . sa lang ist. Also ist S' = S. 
Aufgaben:
Hinweis: Bei den folgenden Konstruktionsaufgaben ist es erlaubt 2/3 einer
Strecke auszumessen.
- Konstruiere ein Dreieck von dem gegeben sind:
- sb = 6.6cm, sc = 4.8cm udn a = 6.9cm.
- sb = 6cm, sc = 3.3cm und b = 5.8cm.
- hc = 4.2cm sc = 4.5cm und hc = 4.2cm
- sa = 6.6cm, sb = 4.5cm und hc = 4.2cm.
- Konstruiere ein Dreieck aus:
- hc = 4.2cm
alpha=350 und beta=350
- Inkreisradius r = 1.6 cm
alpha = 400 und
beta = 760
- Umkreisradius r = 3.5cm hc = 4.1cm und c = 6.4cm.
- b = 7.2cm sb = 4.2cm und ha = 6.4cm
- c = 6.2 cm, ha = 3.6cm und hb = 5.7cm.
- Beweise, dass in jedem Dreieck gilt:
- Ist a = b, so ist
sa = sb.
- Ist
sa = sb so ist a = b.
- Konstruiere ein gtelichschenkliges Dreieck aus der Seitenhalbierenden
sa und der Basis c.
- Konstruiere ein Dreieck aus einer Seite (7cm), einer Höhe (4.5cm)
und einer Seitenhalbierenden (5cm). Unterscheidung von 5 Fällen.
- Gegeben sind drei sich schneidende Geraden und auf einer derselben ein
Punkt A. Zeichne ein Dreieck, das A zur Ecke hat, bei dem B und C
auf den beiden andern Geraden liegen und in dem P
- dder Höhenschnittpunkt
- Umkreismittelpunkt
- der Schwerpunkt ist.
- Konstruiere ein Dreieck von dem gegeben sind:
- Die drei Seitenmitten
- Zwei Ecken A und B und der Höhenschnittpunkt H.
- Zwei Ecken A und B und der Schwerpunkt S.
- Zwei Ecken A und B und der Inkreismittepunkt M.
- Die Ecke A, der Schwerpunkt S und der Umkreismittelpunkt U.
- Im Dreieck ABC sei D die Seitenmitte von [BC]. Ziehe durch D
die Parallele zu AC und AB. Welche der entsehenden Teildreiecke sind
kongruent und warum.
- Zeige: Die Seitenmitten eines beliebigen Vierecks bilden ein
Parallelogramm.
- Gegeben sei ein Parallelogramm mit den Eckpunkten ABCD. Die
Eckpunkte liegen auf den Seiten eines Vierecks RFGH und zwar derart,
dass A Seitenmitte von [HF], B Seitenmitte von [EF] und C
Seitenmitte von [FG] ist.
Zeige D ist Seitenmitte von [GH].
- Ist ein Viereck eindeutig aus seinen Seitenmitten konstruierbar?
- Konstruiere ein Fünfeck aus seinen Seitenmitten.
- Zeige allgemein: Jedes Vieleck ungerader Eckenzahl ist aus seinen
Seitenmitten konstruierbar.
- Gegeben ist ein Dreieck ABC. Verlängert man die Seite b über A hinaus um
b, so erhält man den Punkt A'. Verlängert man die Seite a über B
hinaus um a, so erhält man B'. Zeige: A'B' ist parallel zu AB
-
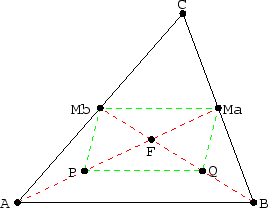
Abbildung 3.13:
Parallele
 |
In der Skizze ist [CA'] zweimal so lang wie [CA] und [CB']
zweimal so lang wie [CB]. Zeige A'B' ist parallel zu AB.
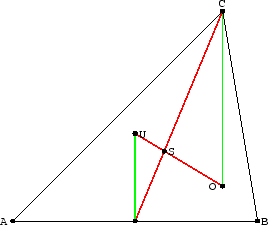
- Im DReieck sei S der Schnittpunkt der Seitenhalbierenden. U der
Umkreismittelpunkt und O liege auf US, so dass [OS] doppelt so lang
wie [US] ist. Zeige: O liegt auf der Höhe auf die Seite [AB].
Abbildung 3.14:
Eeuler Gerade
 |
Beweise: Umkreismittelpunkt, der Schnittpunkt der Seitenhalbierenden und der
Höhemschnittpunkt liegen auf einer Geraden.
Dieser schöne Satz stammt von Leonard Euler georen am 15.04.1707 in Basel. Er
starb am 18.9.1783 in Petersburg.
- Konstruiere ein Dreieck von dem gegeben sind:
- a + b = 10.4cm, c = 8cm und
alpha= 380
- a + c = 13.2cm, b = 6cm und hc = 2.7cm.
- a + b = 11cm, c = 7.2cm und
gamma= 720
- Schlage um den Umkreismittelpunkt M eines gleichseitigen Dreiecks
einen Kreis mit beliebigem Radius. Beweise, dass von den 6 Schnittpunkten
des Kreises mit den Seiten je 3 ein gleichseitiges DReieck bilden.
Andreas Bartholome
2003-11-28