Next: Programme Up: Lösungen Previous: Zu Kapitel 2
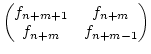 ,...].
,...].
Beweis:
Es sei
a0 = ![]() + a und a1 = 1. Dann ist
+ a und a1 = 1. Dann ist
![]()
![]()
![]() = [
= [![]() + a] = 2a. Denn
a2 < a2 + 1 und
a2 +1 < (a + 1)2. Daher ist
+ a] = 2a. Denn
a2 < a2 + 1 und
a2 +1 < (a + 1)2. Daher ist
![]() < a + 1.
Also ist
[
< a + 1.
Also ist
[![]() ] = a und damit
[
] = a und damit
[![]() + a] = 2a. Es ist
a2 = a0 -2 . a . 1 =
+ a] = 2a. Es ist
a2 = a0 -2 . a . 1 = ![]() - a und
- a und
![]() =
= ![]() =
= ![]() + a.
+ a.
Beh: Für alle
n ![]()
![]() gilt:
gilt:
| = | |||
| = | |||
| = | |||
| = | 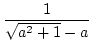 + a. + a. |
Andreas Bartholome