Satz 3.4.1 (Kettenregel)
Sei
f : A 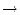 B und
g : B
B und
g : B 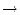 C Funktionen. f sei
differenzierbar an der Stelle s und g sei differenzierbar an der
Stelle f (a).
Dann ist gof differenzierbar an der Stelle a und es
gilt
(gof )'(a) = g'(f (a)) . f'(a).
C Funktionen. f sei
differenzierbar an der Stelle s und g sei differenzierbar an der
Stelle f (a).
Dann ist gof differenzierbar an der Stelle a und es
gilt
(gof )'(a) = g'(f (a)) . f'(a).
Beweis:Zunächst führen wir den Beweis nur in dem besonders einfachen
Fall durch, dass f monoton wachsend ist.
Wir betrachten wieder die Sekantensteigungsfunktion.
Ist x 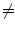 a, so ist
f (x)
a, so ist
f (x) 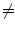 f (a), da f streng monoton
wachsend vorausgesetzt ist.
Ist (an) eine Folge, deren Limes a ist, so ist
f (a), da f streng monoton
wachsend vorausgesetzt ist.
Ist (an) eine Folge, deren Limes a ist, so ist
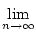 f (an) = f (a).
Die Folge
(yn) = (f (an)) ist daher eine Folge mit
f (an) = f (a).
Die Folge
(yn) = (f (an)) ist daher eine Folge mit
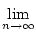 f (an) ist also eine Folge mit dem
Grenzwert f (a). Da g an dieser Stelle differenzierbar ist, konvergiert
der erste Faktor in der obigen Gleichung 3.1
gegen g'(f (a))'. Da f differenzierbar an der Stelle a ist, konnvergiert
der zweite Faktor in
f (an) ist also eine Folge mit dem
Grenzwert f (a). Da g an dieser Stelle differenzierbar ist, konvergiert
der erste Faktor in der obigen Gleichung 3.1
gegen g'(f (a))'. Da f differenzierbar an der Stelle a ist, konnvergiert
der zweite Faktor in
![[*]](crossref.png) gegen f'(a).
Damit folgt die Behauptung des Satzes.
gegen f'(a).
Damit folgt die Behauptung des Satzes. 
Unterabschnitte
Andreas Bartholome
2003-11-26
![[*]](crossref.png) gegen f'(a).
Damit folgt die Behauptung des Satzes.
gegen f'(a).
Damit folgt die Behauptung des Satzes.