Satz 3.2.1
- Seien
f, g : A
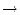 B beide differenzierbar
an der Stelle a
B beide differenzierbar
an der Stelle a 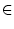 A. Dann ist f + g an der
Stelle a differenzierbar an der Stelle a
A. Dann ist f + g an der
Stelle a differenzierbar an der Stelle a 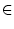 A
und es gilt
(f + g)'(a) = f'(a) + g'(a).
A
und es gilt
(f + g)'(a) = f'(a) + g'(a).
- Ist
c
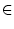
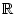 und
f : A
und
f : A 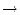 B differenzierbar
an der Stelle a, dann ist c . f an der Stelle a
differenzierbar und es ist
(c . f )'(a) = c . f'(a).
B differenzierbar
an der Stelle a, dann ist c . f an der Stelle a
differenzierbar und es ist
(c . f )'(a) = c . f'(a).
Beweis:Zu 1. Sei (an) eine Folge, deren Grenzwert a ist.
Dann gilt:
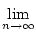
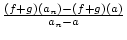 =
= 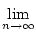
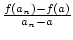 +
+ 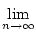
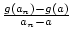 = f'(a) + g'(a).
= f'(a) + g'(a).
Zu 2. Dies ist noch einfacher.

Satz 3.2.2
Ist f an der Stelle a differenzierbar, so ist f dort stetig.
Beweis:Sei (an) eine Folge, die gegen a konvergiert.
Dann existiert der Grenzwert der Folge
(bn) = 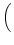
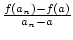
 .
Wir erhalten
f (an) - f (a) = (an - a) . bn.
Beide Faktoren der Folge sind konvergent. Der erste Faktor ist eine
Nullfolge. Daher ist die
f (an) - f (a) eine Nullfolge.
Dies bedeutet, dass
.
Wir erhalten
f (an) - f (a) = (an - a) . bn.
Beide Faktoren der Folge sind konvergent. Der erste Faktor ist eine
Nullfolge. Daher ist die
f (an) - f (a) eine Nullfolge.
Dies bedeutet, dass
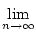 f (an) = f (a) ist.
Dies hinwiederum bedeutet, dass f stetig an der Stelle a ist.
f (an) = f (a) ist.
Dies hinwiederum bedeutet, dass f stetig an der Stelle a ist. 
Satz 3.2.3 (Produktregel)
Seien f, g an der Stelle a diffeerenzierbare Funktionen.
Dann ist f . g an der Stelle a differenzierbar und
es gilt:
(f . g)'(a) = f (a) . g'(a) + f'(a) . g(a).
Beweis:Wir betrachten zunächst wieder die zur Produktfunktion
gehörende Sekantenfunktion.
sek(x, a) = 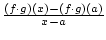 =
= 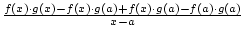
Setzt man nun für x eine Folge ein, die gegen a strebt, so
sieht man, dass der erste Summand
gegen g'(a)f (a) konvergiert und der zweite gegen
g(a)f'(a). 
Satz 3.2.4 (Quotientenregel)
Seien
f, g : 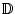
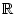 zwei an der Stelle a differenzierbare
Funktionen und es gelte
g(a)
zwei an der Stelle a differenzierbare
Funktionen und es gelte
g(a) 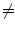 0. Dann ist
0. Dann ist
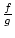 an der
Stelle a differenzierbar und es gilt:
an der
Stelle a differenzierbar und es gilt:
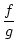
'(
a) =
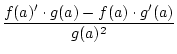
.
Beweise diese Aussage selbstständig.
Andreas Bartholome
2003-11-26
![]()
![]() =
= ![]()
![]() +
+ ![]()
![]() = f'(a) + g'(a).
= f'(a) + g'(a).
![]()
![]() =
= ![]()
![]()
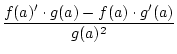 .
.