Wir erklären den Begriff der Sekantensteigung an
der Stelle a in Abhängigkeit von x:
Definition 3.1.1
Sind a und x aus dem Definitionsbereich der
Funktion f, so heißt
sek(x, a) = 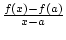 Sekantensteigung
an der Stelle a.
Dies ist eine
Funktion von x!
Sekantensteigung
an der Stelle a.
Dies ist eine
Funktion von x!
Beispiel:
f (x) = x2
sek(a, x) = 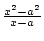 = x + a.
,,Strebt`` nun x gegen a, so strebt sek(a,x) gegen 2a.
Genauer: Ist (xn) irgend eine Folge deren
Grenzwert a ist, so ist der Grenzwert der Folge
sek(a, xn) = 2a. Anschaulich wird aus der Sekante
beim Annähern eine Tangente
= x + a.
,,Strebt`` nun x gegen a, so strebt sek(a,x) gegen 2a.
Genauer: Ist (xn) irgend eine Folge deren
Grenzwert a ist, so ist der Grenzwert der Folge
sek(a, xn) = 2a. Anschaulich wird aus der Sekante
beim Annähern eine Tangente
Definition 3.1.2
Eine Funktion
f : A 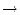 B
B 
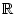 heißt differenzierbar an
der Stelle a
heißt differenzierbar an
der Stelle a 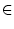 A genau dann, wenn es eine Zahl c gibt, so dass
für jede Folge (an) mit
A genau dann, wenn es eine Zahl c gibt, so dass
für jede Folge (an) mit
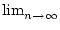 an = a gilt:
an = a gilt:
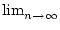 sek(an, a) = c. Die Zahl c heißt dann
Ableitung an der Stelle a. Bezeichnung: f'(a) oder
sek(an, a) = c. Die Zahl c heißt dann
Ableitung an der Stelle a. Bezeichnung: f'(a) oder
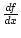 (a).
f'(a) heißt auch Steigung der Tangente im Punkt (a, f (a)).
(a).
f'(a) heißt auch Steigung der Tangente im Punkt (a, f (a)).
Unterabschnitte
Andreas Bartholome
2003-11-26
![\includegraphics[height=5cm width=10cm]{/home/andreas/tex/schule/elfte/bild/bild7}](img230.png)
![]() = x + a.
,,Strebt`` nun x gegen a, so strebt sek(a,x) gegen 2a.
Genauer: Ist (xn) irgend eine Folge deren
Grenzwert a ist, so ist der Grenzwert der Folge
sek(a, xn) = 2a. Anschaulich wird aus der Sekante
beim Annähern eine Tangente
= x + a.
,,Strebt`` nun x gegen a, so strebt sek(a,x) gegen 2a.
Genauer: Ist (xn) irgend eine Folge deren
Grenzwert a ist, so ist der Grenzwert der Folge
sek(a, xn) = 2a. Anschaulich wird aus der Sekante
beim Annähern eine Tangente